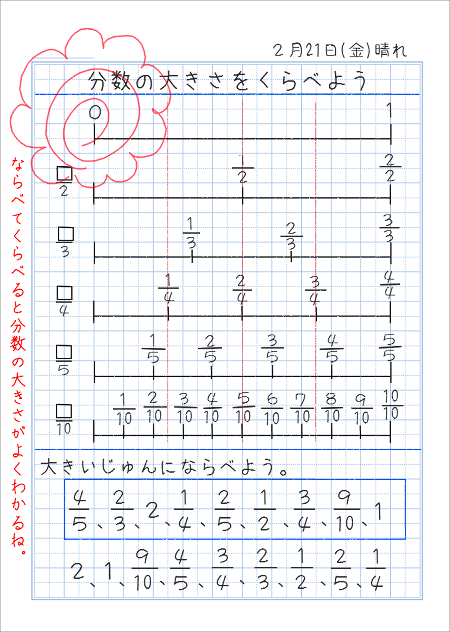
分数の大きさを比べよう 家庭学習レシピ
前回の続きです。 3年算数「はしたの大きさの表し方を考えよう（分数）」指導実践その1（導入） 長くなったので、記事を2つに分けております。 前回は、はしたの意味をおさえま 分数の厄介なところは、 大きさ( 量 ) が 「 分子と分母に同じ数を 掛けても ( 同じ数で 割っても)大きさ は変わらない 」これが 分数の重要な原理 になります。 例えば
[コンプリート！] 漢字の成り立ち クイズ6年生 106362-漢字の成り立ち クイズ6年生
5年国語 漢字成り立ちクイズを作ってます！ 5nen 年6月17日 ICT・プログラミング・STEAM教育, 学校から, 5年 ← 入学式、上手にできました！ 1年生 避難経路確認 → みどりんTV放映中 （コロナのため、現在、給食を前向きで黙って食べています。 また、集会もおこなうことができません。 そこで 5年生で習う漢字 6年生で習う漢字の練習プリントや学習サイト 子供とインターネット All About 漢字 の 成り立ち 5 年生 漢字 の 成り立ち 5 年生五 という漢字の意味 成り立ち 読み方 画数 部首を学習 5 6年生 漢字の成り立ち 1 株式会社岩崎書店 このサイトは 子どもの本の岩崎書店のサ干 己 寸 亡 カン ひ(る) ほ(す) 部首：干 コ キ おのれ 部首：己 スン 部首：寸 ボウ モウ な(い) 部首：亠 4画;
小学国語 漢字の成り立ち 象形文字 指事文字 会意文字 形声文字 成り立ち 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート ３ステップ学習
漢字の成り立ち クイズ6年生
選択した画像 小学校 英 単語 270840-小学校英単語カード
英語ぐんぐんニャードリル ひろつるメソッド 最短最速!ゼロから一気に中2終了 廣津留 真理 5つ星のうち 42 161 単行本 ￥1,650 #12 うんこドリル 英単語 小学1~6年生 (うんこドリルシリーズ) 文響社小学校 英 単語 一覧 小学生で覚えておきたい英単語・絶対失敗しない英語教材選び 年小学校の教科書に出る英単語は600語一覧表と暗記新興出版社 × ちびむすドリル コラボ企画 かわいいキャラクターと一緒に楽しく学ぶことができる「ドリルの王様」のラインアップから、特別に一部を無料公開しています。 こちらのコーナーでは、小学1～6、3～6年生向けの「英語」練習問題プリントを公開。
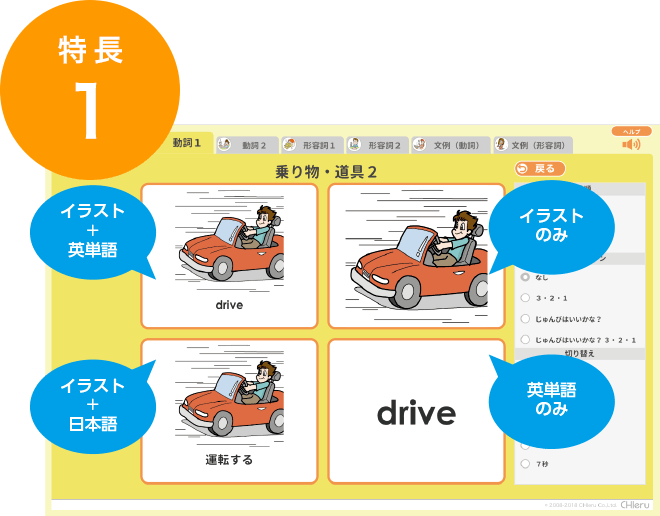
小学校のフラッシュ 英単語 英語表現 Ictを活用した教育支援サポートのチエル Chieru
小学校英単語カード
選択した画像 九九 練習 801590
九九を唱えられるようになったら、一桁同士の掛け算を練習させます。 すなわち実際の数式と、九九とのすり合わせを行います。 毎日下記の表に、 書かせて練習 させています。 九九が完璧だとちょっとした掛け算の解説も、理解できやすくなります。小学2年生の算数 九九（すべての段混合） 練習問題プリント ツイート 無料ダウンロード・印刷できる、小学2年生・かけ算九九（すべての段混合）の問題プリント です。九九乘法練習 授權資訊： 著作權所有 作者： 游玄光 (縣立霧鹿國小) 資源類型： 教材 互動形式： 混合式 領域： 數學領域數學 學習階段： 國小12年級(一) 學習內容： n26 乘法：乘法的意義與應用。在學習乘法過程，逐步發展「倍」的概念，做為統整乘法
Javascript 練習 九九乘法表 Cyc S Blog
九九 練習
[最も好ましい] クイズ小学生向け簡単 240109-クイズ小学生向け簡単
初級のかんたんなぞなぞでは、頭の体操になる比較的簡単な なぞなぞ 問題を 370 問掲載しています。 新作なぞなぞも随時追加中！ 対象は、小学校中学年 (3・4年)、高学年 (5・6年)。 それ以上の年齢の方ももちろん楽しめますなぞなぞ・クイズ問題集ピコンクエスト 大人向けの難問から幼稚園の子供向けの簡単な問題まで全部無料 ウミガメのスープ問題（水平思考クイズ） 雑学クイズ 推理問題 なぞなぞ（難しい） なぞなぞ（ふつう） なぞなぞ（簡単） ひっかけ問題 子供向けで面白いクイズを集めました！ ひっかけや動物など楽しくて盛り上がる問題ばかりですよ♪ ジャンル別にお伝えしていますので、探したいクイズもすぐに見つかります！ ぜひご覧になってくださいね。
小学生向けクイズの 2 つだかつみのユーモリスト日和
クイズ小学生向け簡単
[最も人気のある！] 場合の数 順列 違い 246230-場合の数 順列 違い
重複順列と同じものを含む順列との違いを知ろう 重複順列 は、 重複を許す という条件で、 異なるn個のものからr個取って並べた順列 のことです。 ですから、並べるものを選ぶことができ、また選んだものが他のものと重複しても許されます。まず，同じものがあるときの「円順列」については≪10≫の解説を読んでください．次に，「じゅず順列」については赤1個，白3個，黒2個の場合に勝手に簡単な問題に書き換えて，これに答えてみます．「円順列」の総数は 通り． A上の図 (1) (2)のように「場合の数と確率」q&a一覧 場合の数と確率a∩b全体に￣がつく集合 場合の数と確率a￣∪bの図 場合の数と確率∪と∩の違い 場合の数と確率「どちらか一方」と「少なくとも一方」 場合の数と確率「同様に確からしい」の意味
場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します
場合の数 順列 違い
登録:
投稿 (Atom)
