確認してくださいね 中2数学「平行四辺形の証明」の問題 どこよりも簡単な解き方・求め方 前回までで「平行四辺形」の「定義」「性質」「なるための条件」を学習してきました 今回はその他の「平行四辺形の証明」を一緒にやっていきましょう証明 1.長方形の対角線の長さは等しい。 ABCと DCBで 平行四辺形なので AB=DC 1 BC=CB(共通) 2 長方形なので ∠ABC=∠DCB=90° 3 1、2、3より、2辺とその間の角が、それぞれ等しいので ABC≡ DCB よって AC=DB <戻る> 2.ひし形の対角線は垂直に交わる。 ABOと ADOで ひし形なので AB=AD 1 ひし形は平行四辺形なので BO=DO 2 AO=AO(共通) 3 1、2、3より3辺がそれぞれ等し証明しなさい。 〔証明〕 (3) さらに,二等辺三角形の頂角の二等分線の性質に発展させます。 〔証明〕 (4) 証明されたことがらのうち,大切なものを『定理』といいます。 (2),(3)で証明されたことを『定理』にしてまとめます。
特別な平行四辺形の定義 性質 問題の解き方を伝授するぞ 数スタ
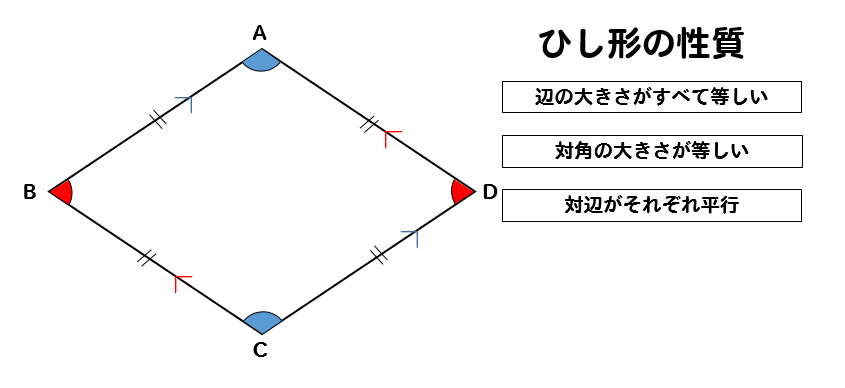
ひし形 性質 証明
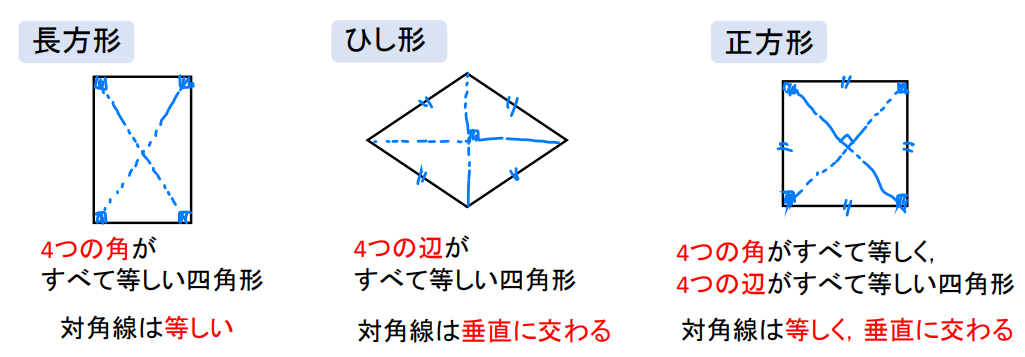
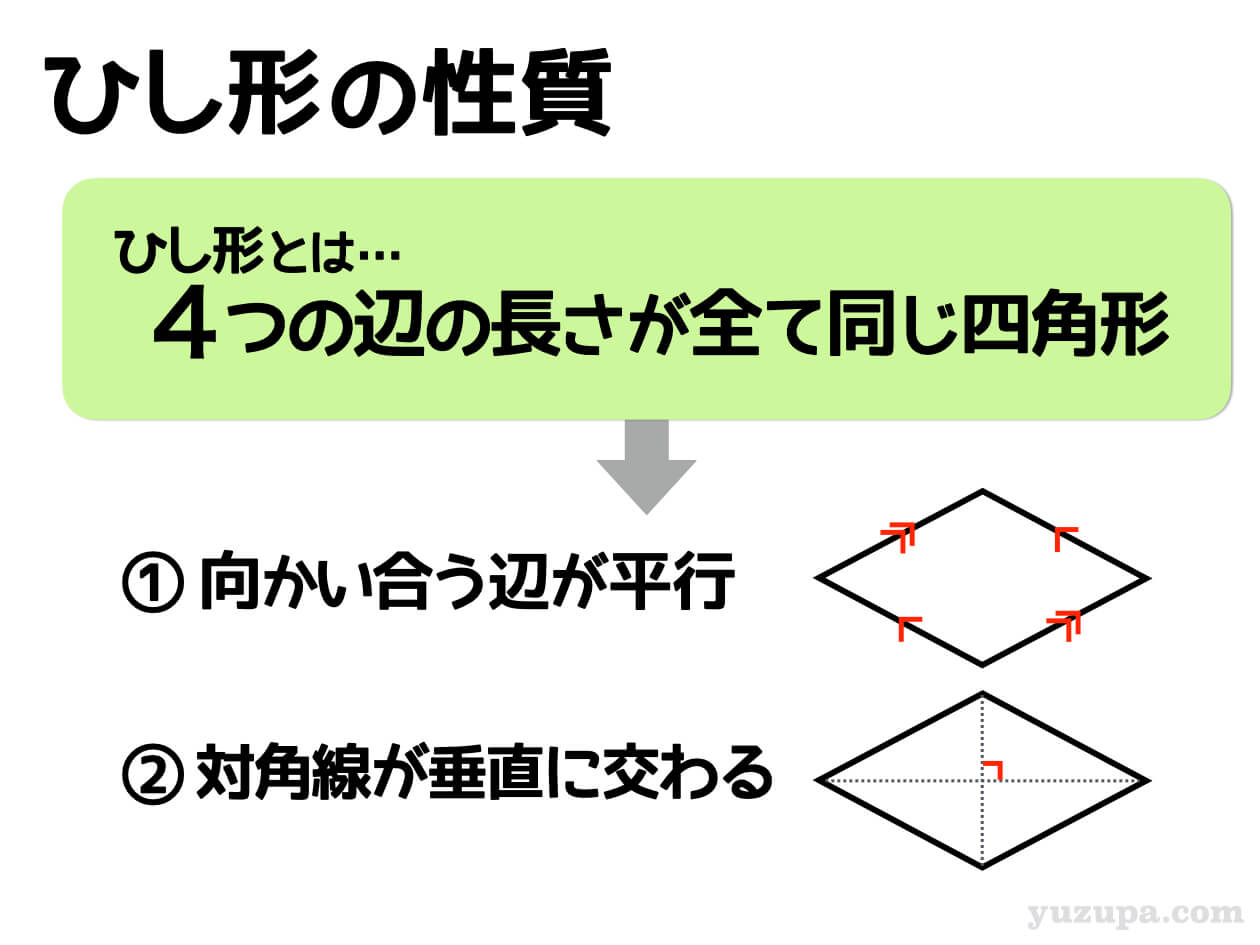
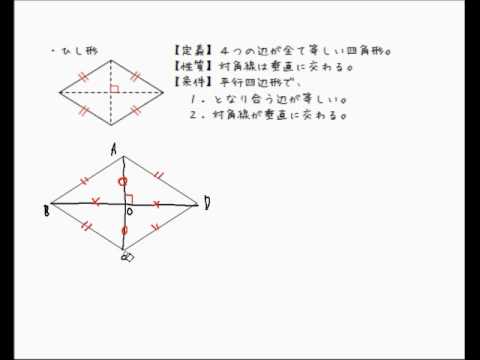
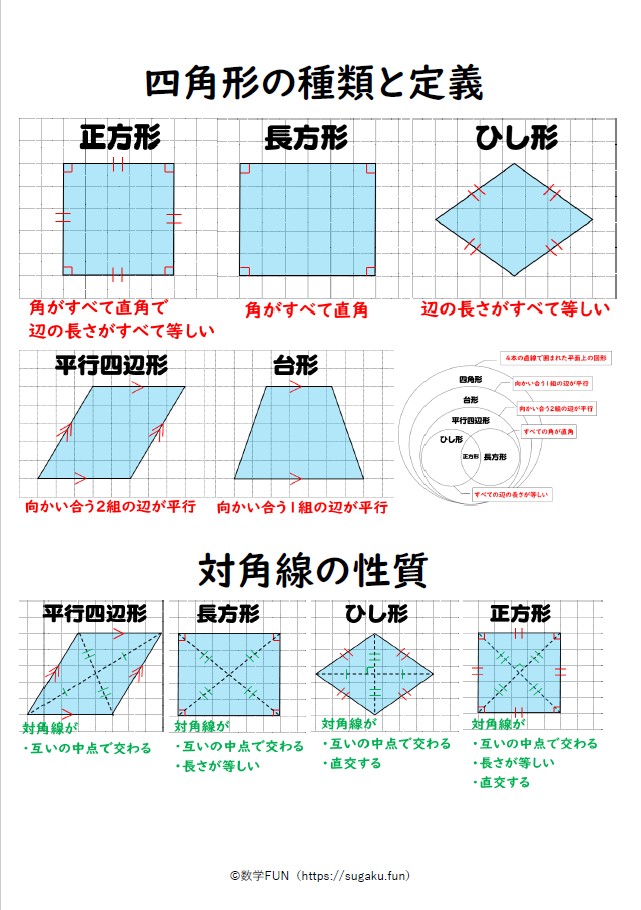
ひし形 性質 証明-②ひし形 定義:4つの辺が等しい四角形をひし形という。 性質:ひし形の対角線は垂直に交わる。 ③正方形 定義:4つの角が等しく、4つの辺が等しい四 角形を正方形という。 性質:正方形の対角線は長さが等しくかつ垂 直に交わる。 q!e ý0û Oá0û MOá0ûN長方形の性質 対角線が等しい ひし形の性質 対角線が垂直に交わる 正方形の性質 対角線が等しく,垂直に交わる 3 学 年 2年 図形の性質と証明⑨いろいろな四角形b 中学校数学・ワークブック 解答 中学校数学 2b5-9b 年 組 氏名



長方形とひし形
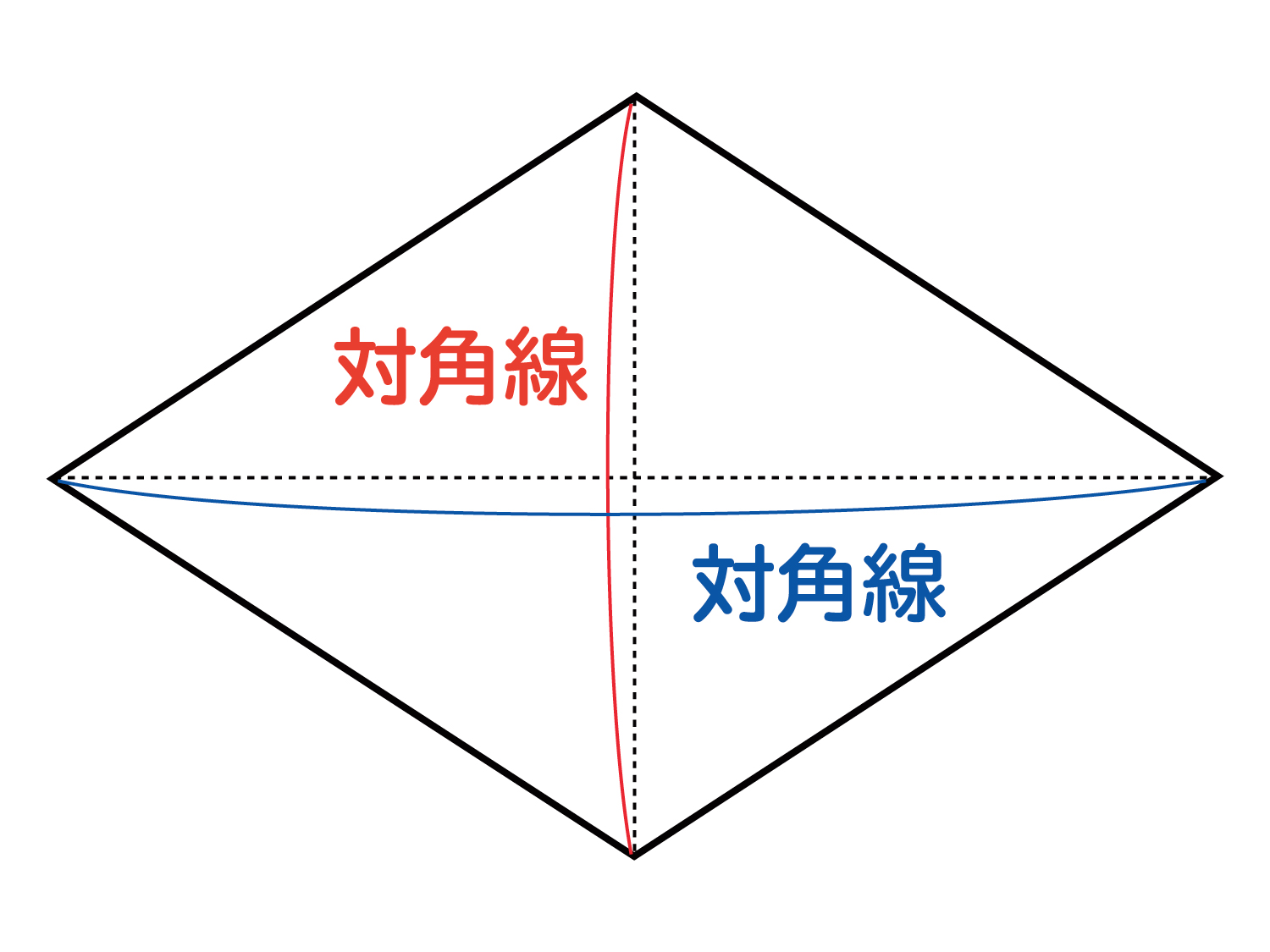
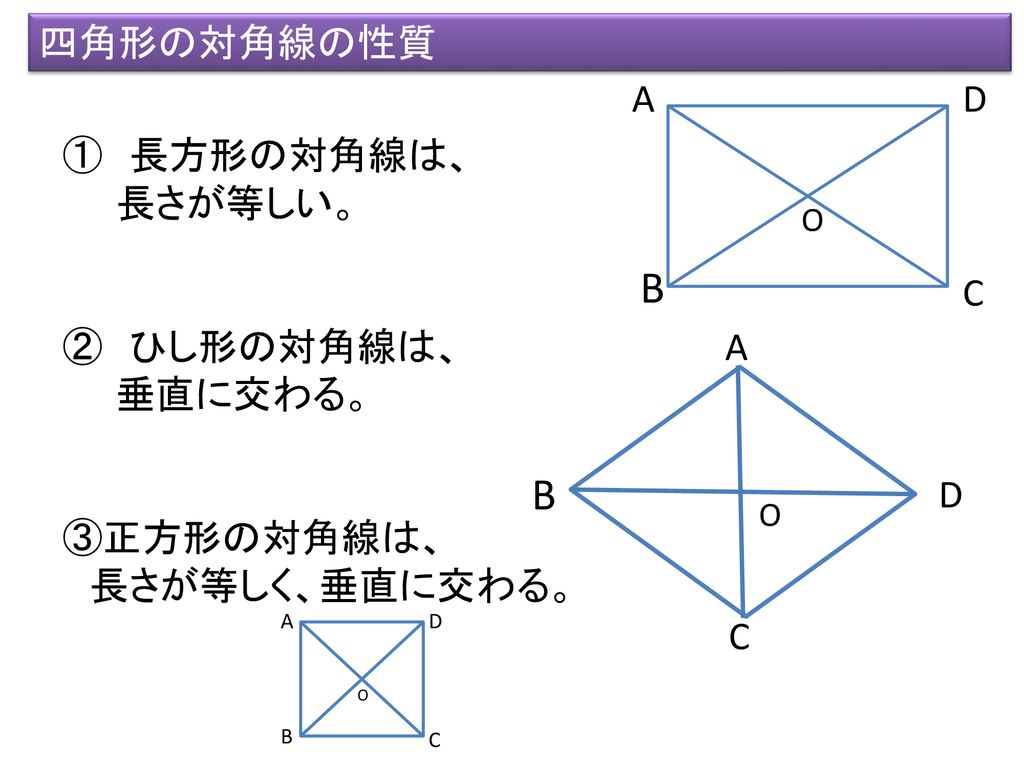
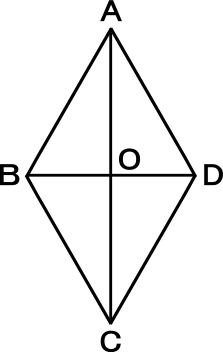
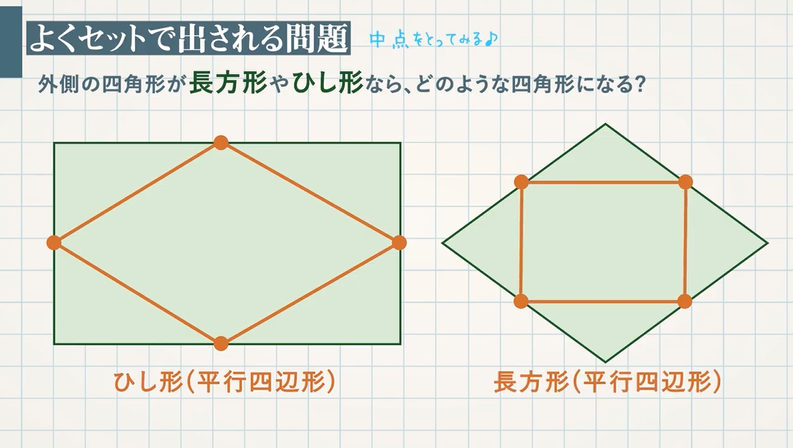
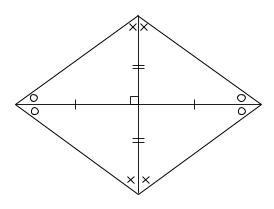
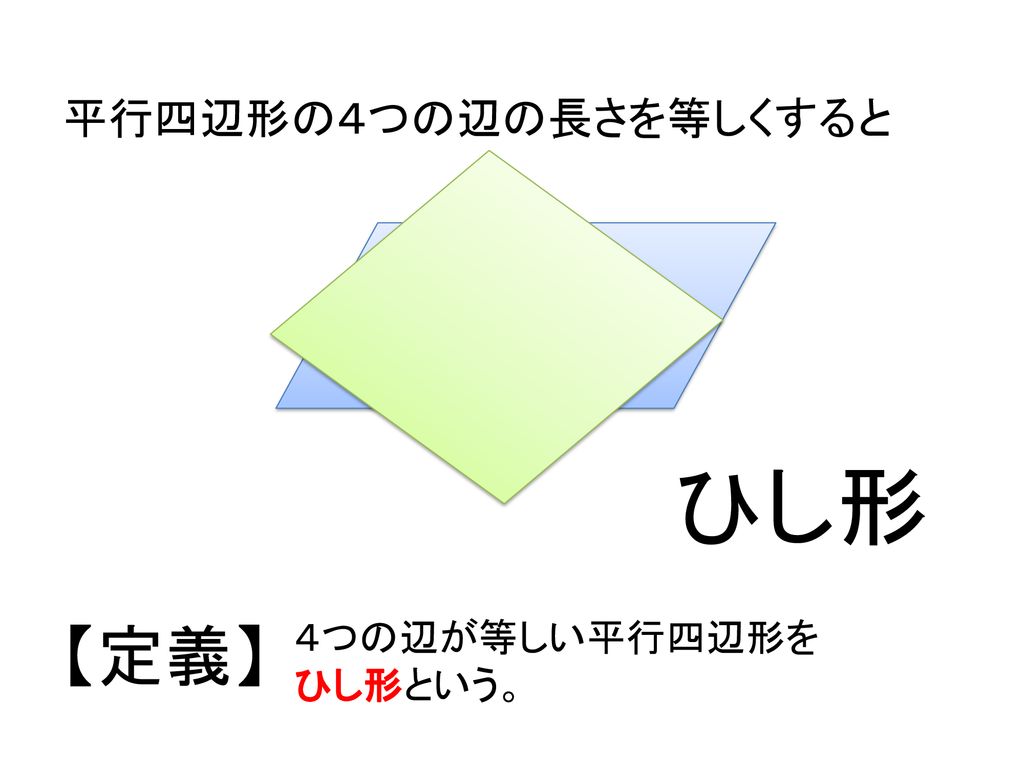
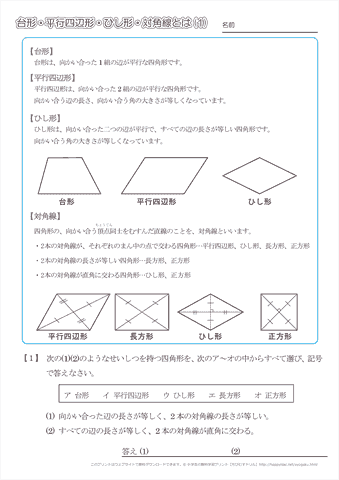
四角形のそれぞれの対角線の性質についてまとめると以下の通り。 それぞれの四角形の対角線の性質 平行四辺形: 対角線が 互いの中点で交わる 長方形: 対角線が 互いの中点で交わる & 長さが等しい ひし形: 対角線が 互いの中点で交わる & 直交する 正方形: 対角線が 互いの中点で交わる & 直交する & 長さが等しい 台形: 特になし 平行四辺形は2本の対角線がそれぞれの真ん中で交わります 3分でわかる! ひし形(菱形)の定義 教科書によると「ひし形の定義」は、 4つの辺がすべて等しい四角形 だ。 ぜんぶの辺が等しい四角形。 ちょうどダイアモンドみたいなやつだね。 これが「ひし形」ってわけさ。 2つの辺がそれぞれ等しいだけだと ・ひし形の性質をまとめる。 ・ひし形をかく。 ・正方形とひし形の共通した特徴を調 べ,ひし形の理解を深める。 考辺の位置関係,辺の 長さ,角の大きさに 着目 ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係 図形 ひし形
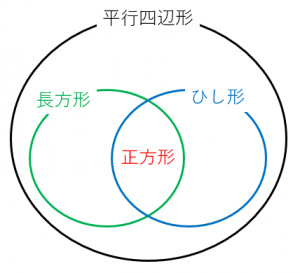
平行四辺形と長方形とひし形と正方形の関係💛 実はこの4つの四角形、兄弟って感じの関係です。 goalに近づくにつれ性質が細かくなっていきます。 長方形 定義『4つの角がすべて等しい四角形』 定理「長方形の対角線は、長さが等しい」 ひし形ひし形 正方形 二組の平行線で囲まれる図形(平行四辺形,長方形,ひし形,正方形)では隣り合う角の和は180°になります.台形(当脚台形も)はそうとは限りません. →閉じる← 6. 2組の対角の大きさが各々等しい. 台形2年生5章 図形の性質と証明(重要問題)全国国公私立入試過去問より ※図形の定義、面積の和、回転体の体積1( )組( )番 名前( ) / 2 2 a 11 • AB = da 、 BC = b cm と する 。 人 g 、 p y • PA B の 高 さ を 図 の よう に とり (A) ひし形 の 性質 で L a て する
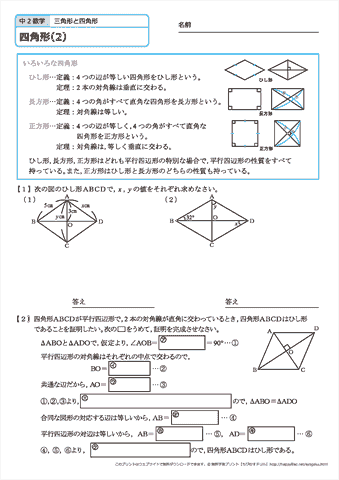
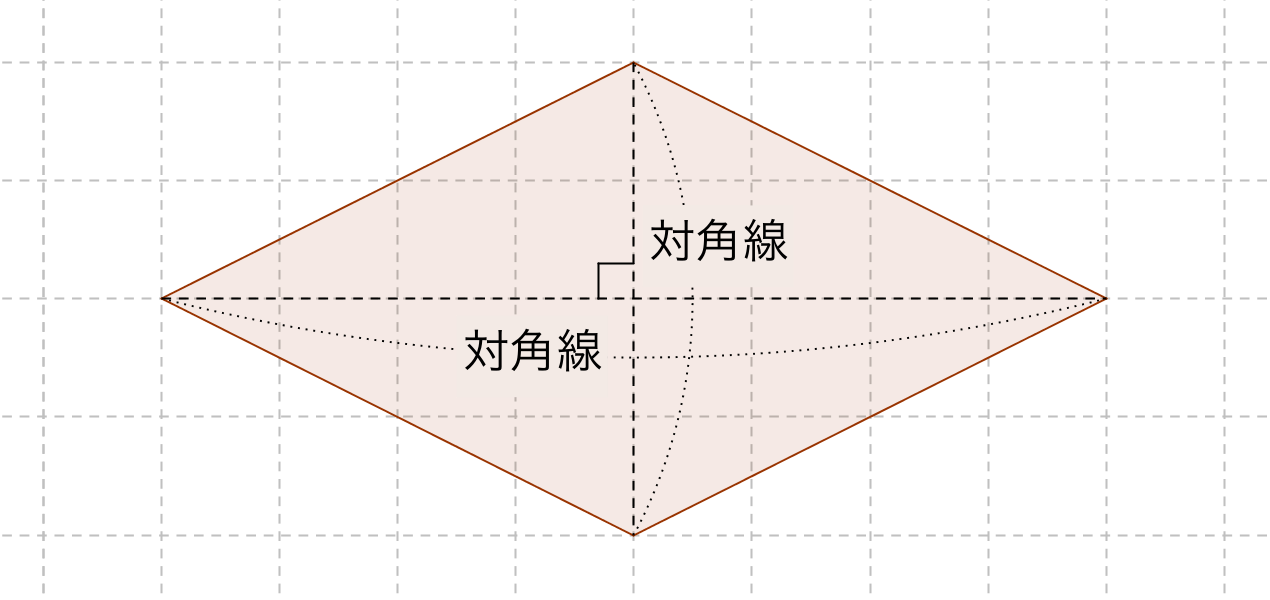
数学25章図形の性質と証明「平行四辺形の性質」<基本問題②> 組 番 名前 1次の図の中から,台形,平行四辺形,長方形,ひし形,正方形をすべて選び記号で答えなさい。 「レポート課題で、要点をまとめました。気に入って頂けたら、♡・コメント・フォローをお願いします☆お待ちしています♬ ※平行線と面積のところは入っていません。」, キーワード 図形の性質と証明,二等辺三角形,正三角形,直角三角形,平行四辺形,長方形,ひし形,正方形②ひし形の対角線は、 。 ③正方形の対角線は、 、 。 下の図に対角線を入れなさい。 四角形の対角線の性質 課題四角形の対角簼の性質を証明しなさい。



中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋




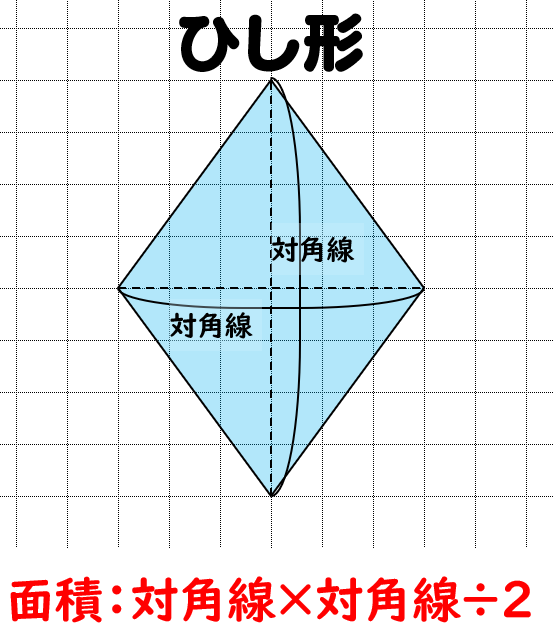
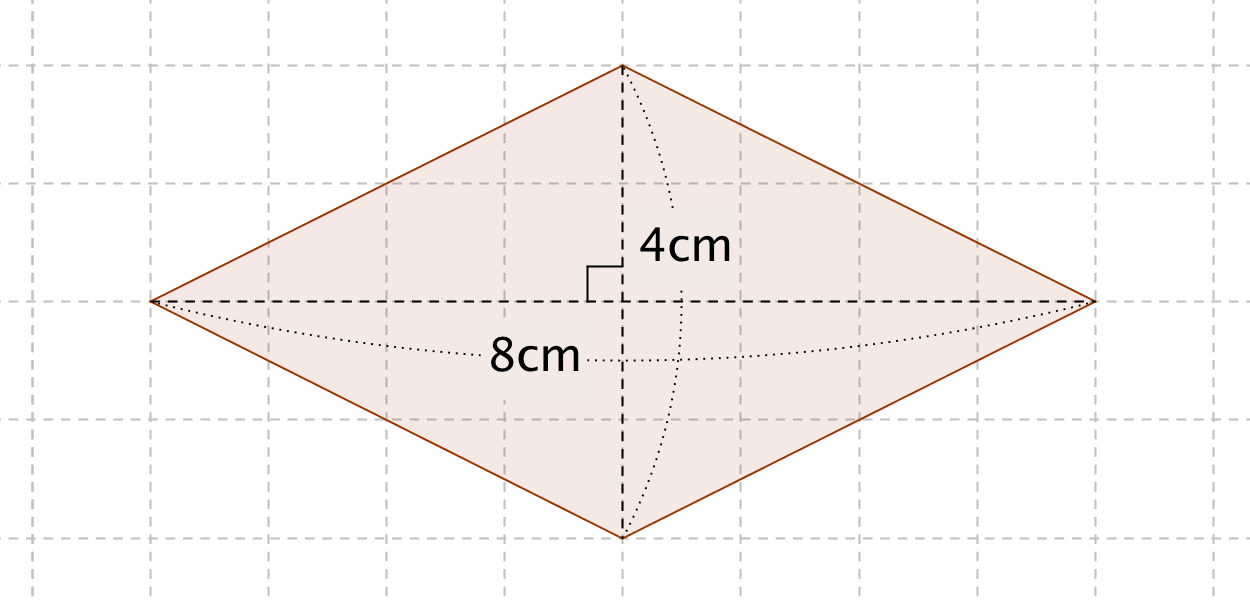
ひし形の面積の求め方 公式と計算例
四角形 の対角線についての性質 1.長方形の対角線の長さは等しい。 ( 証明 ) 2.ひし形の対角線は垂直に交わる。 ( 証明 ) 3.正方形の対角線の長さは等しく、垂直に交わる。 図形を選び、頂点をドラッグして、対角線がどういう条件のとき長方形やひし形になるか調べよう。 長方形 になる条件 対角線の長さが等しく、それぞれの中点で交わるとき、長方形になる。 ( 証明 ) ひし形になる条件単元「図形の性質と証明」の小単元「長方形、ひし形、正方形」における数学的活動を取り入れた授業モデルで す。 下の授業展開案を授業にご活用ください。 単元 図形の性質と証明 (啓林館) 2 四角形図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し




中学校数学 証明のコツ 四角形の性質



図形の性質 作図について 日々是鍛錬 ひびこれたんれん
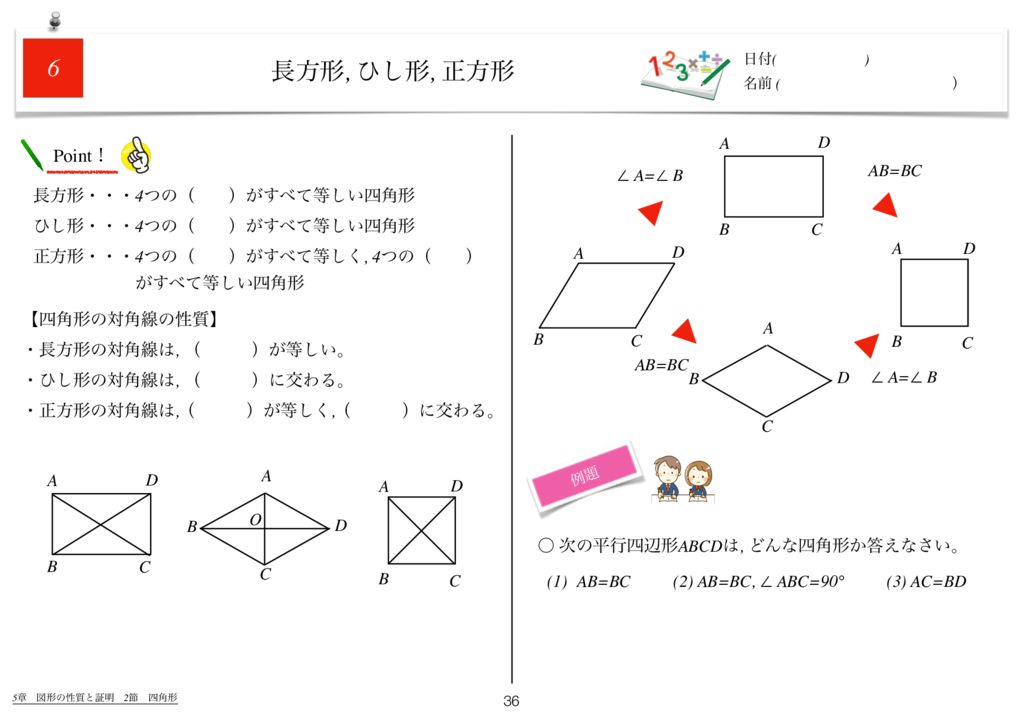
Pocket 今回は中2数学で学習する図形と証明の単元から 「特別な平行四辺形」 について取り上げます。 ここでは「ひし形、長方形、正方形の定義、性質」が問われます。 覚えることが多いですが、問題を解くためのコツを伝授していくのでがんばっていき4つの 内角 が全て等しい菱形は 正方形 であり、その内角は直角に等しい。 目次 1 性質 2 菱形の面積 3 菱形の面のみによる立体 4 シンボル 5 関連項目 性質 菱形は平行四辺形の特殊なタイプであるのでその性質を全て持ちあわせている。 具体的には 2組の対辺は互いに 平行 で長さは等しい 2組の対角の大きさも互いに等しい 対角線がそれぞれの中点で垂直に交わる など。 線対称 な図形であり、 対称軸長方形,ひし形,正方形には,それぞれ次のような性質がある。 > @ 長方形の対角線の ア は等しい。 > @ ひし形の対角線は イ に交わる。 > @ 正方形の対角線は ウ 。



中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋



ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく
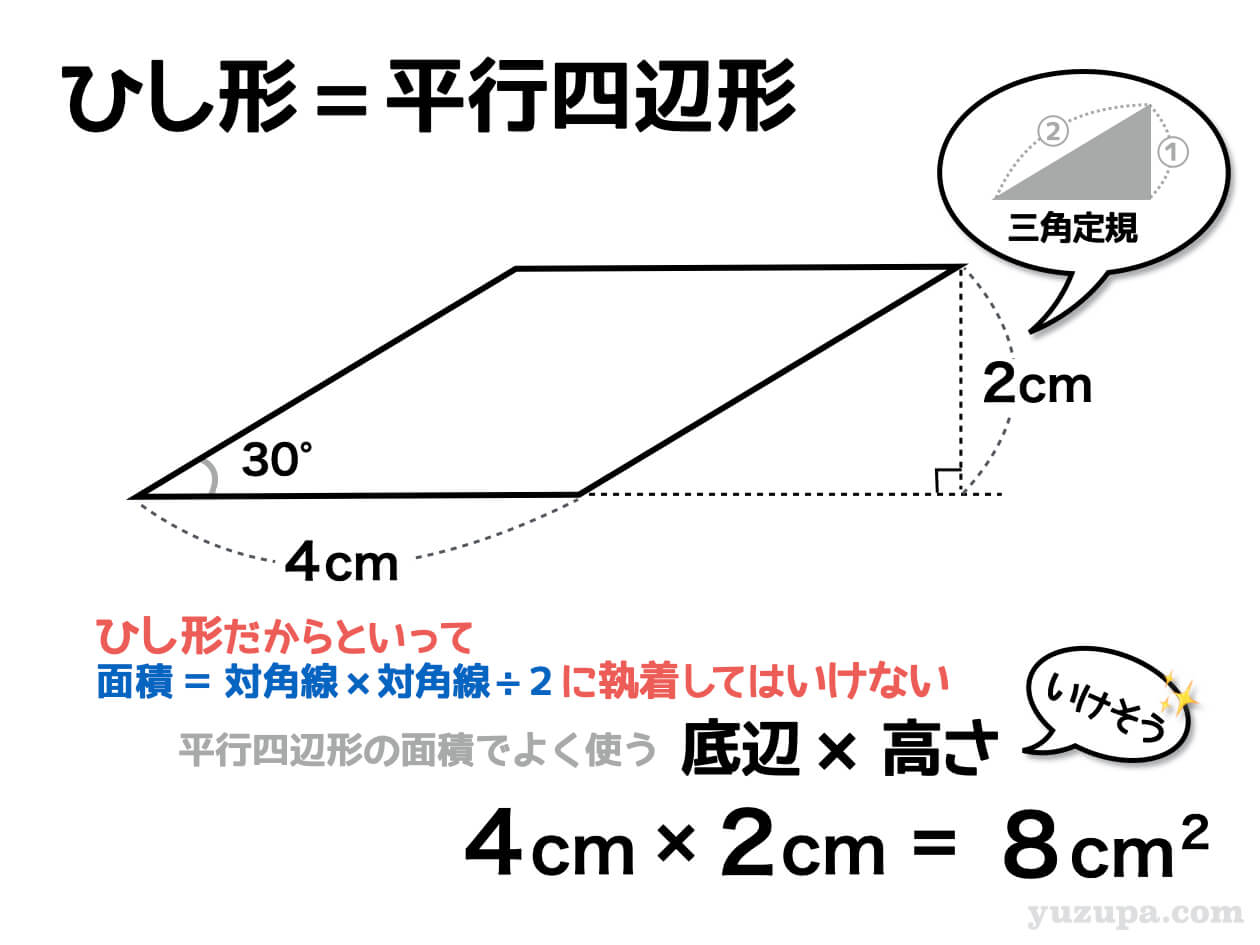
性質② 1 本の対角線がなす三角形の面積比は (上底) (下底) 上底と下底が平行なので、対角線を 本引いてできる つの三角形の高さは等しいですよね。 そのため、 つの三角形の面積比は 上底 下底 となります。 性質③ 2 本の対角線がなす上下の三角形は相似 対角線を 本引くと、台形が 分割されて三角形が つできます。 このうち上下の三角形は、以下の理由から 相似の関係 にあります。という性質も持っています。 覚えておいてください(^^) 平行四辺形とひし形の面積 ひし形は平行四辺形の仲間と言いましたが、面積を求める公式は別々で覚えておきたいものがあります。 特徴を持つ四角形の証明になります。平行四辺形、長方形、ひし形、正方形の特徴を勉強します。 18年3月19日 図形の性質と証明



長方形とひし形



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係
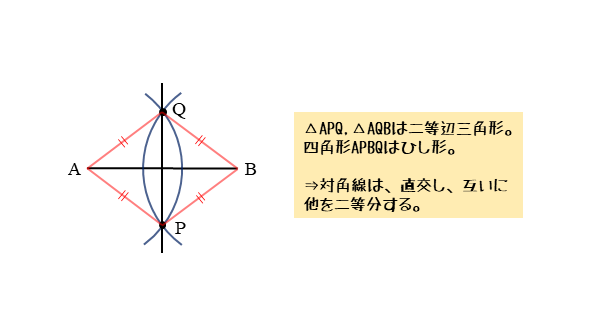
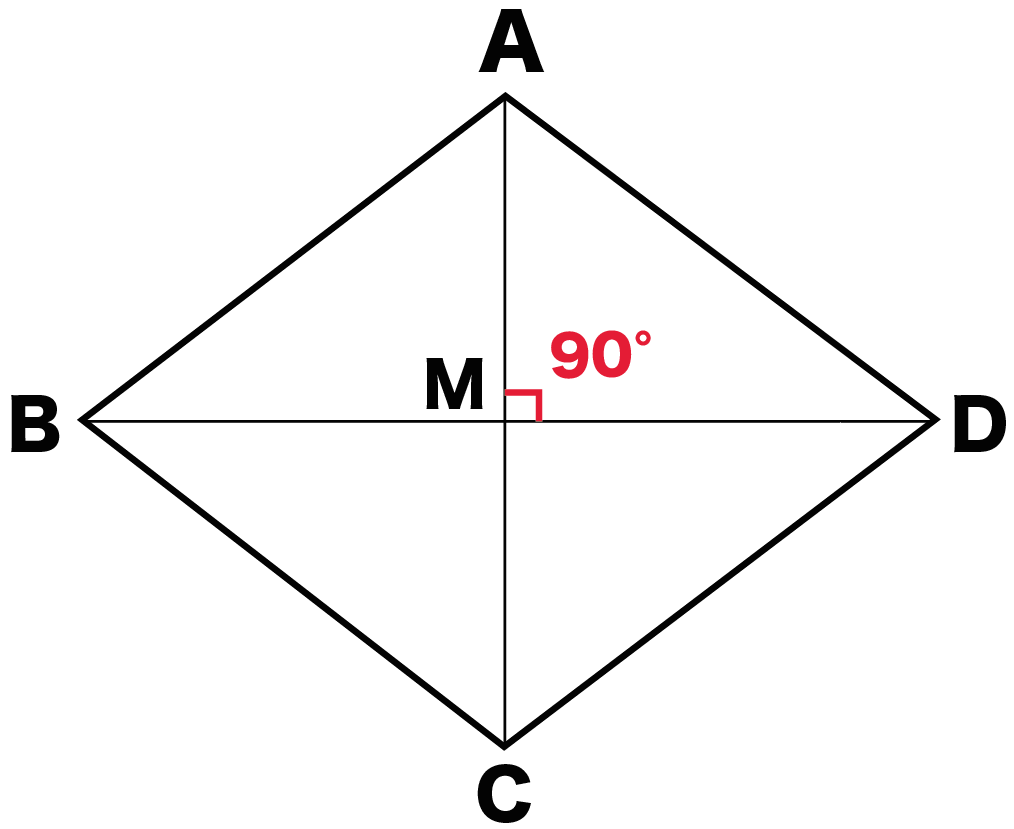
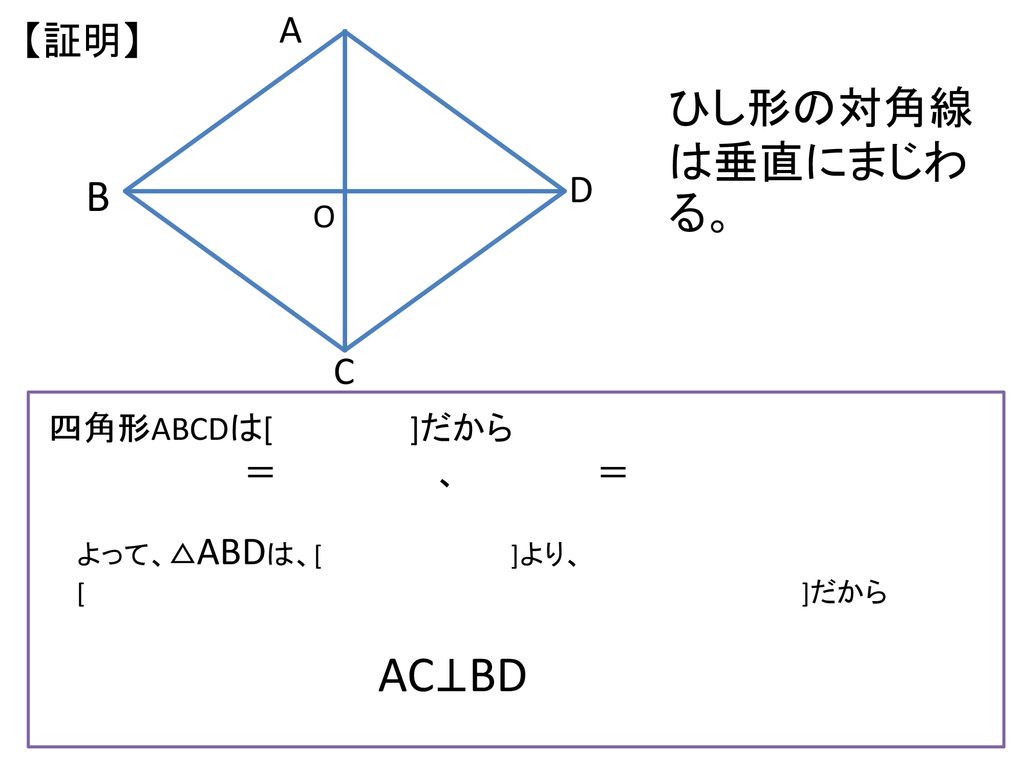
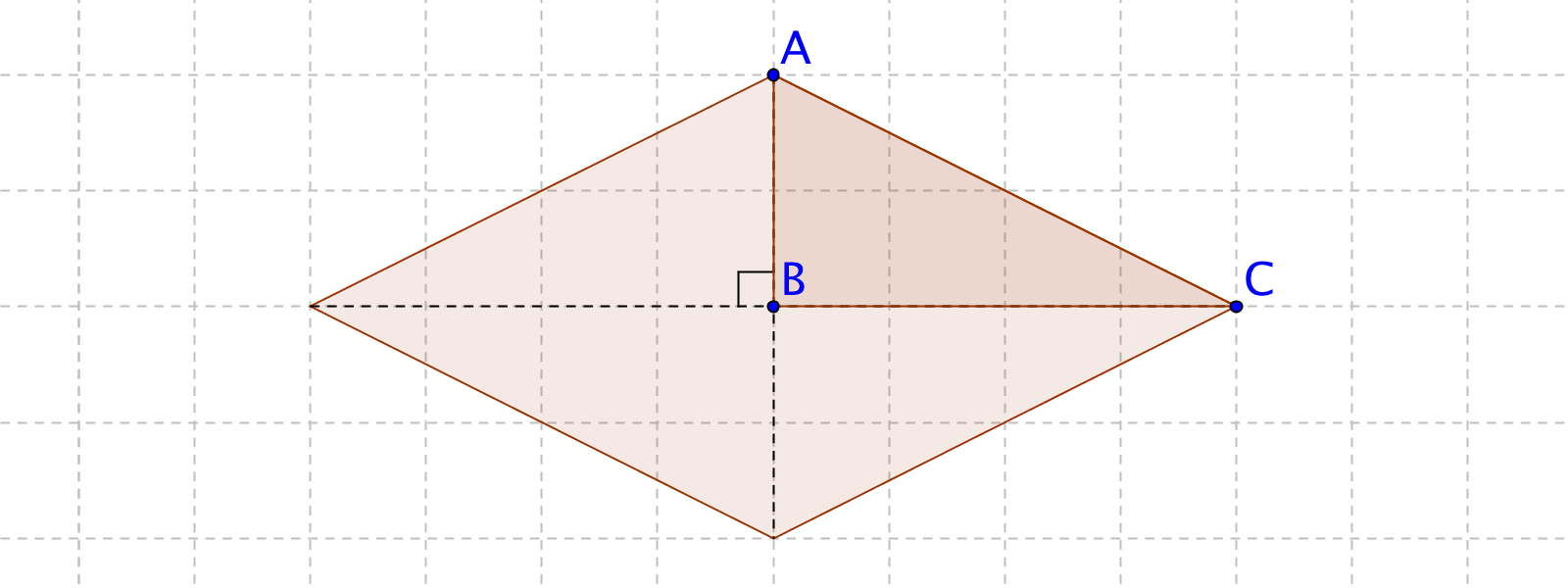
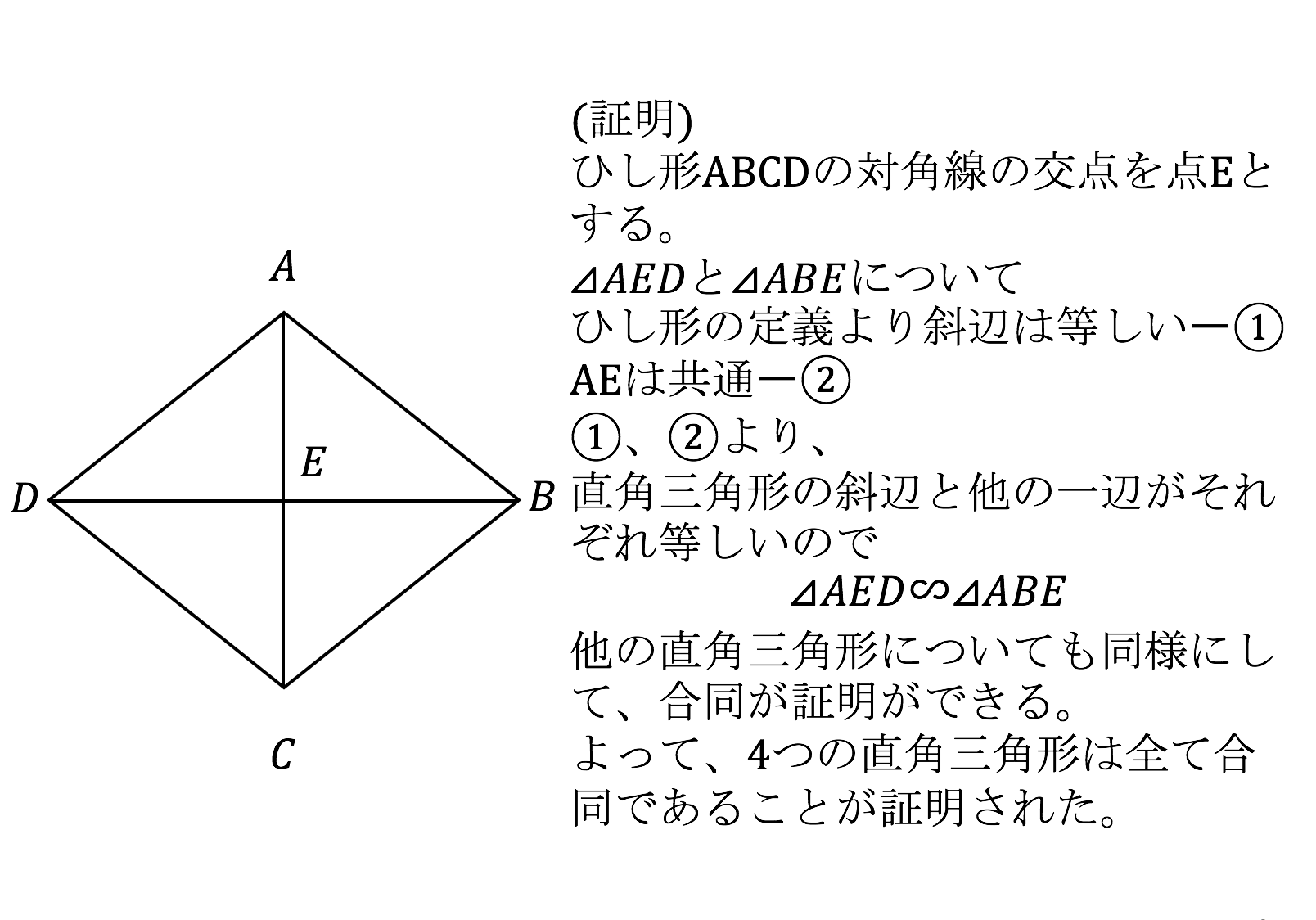
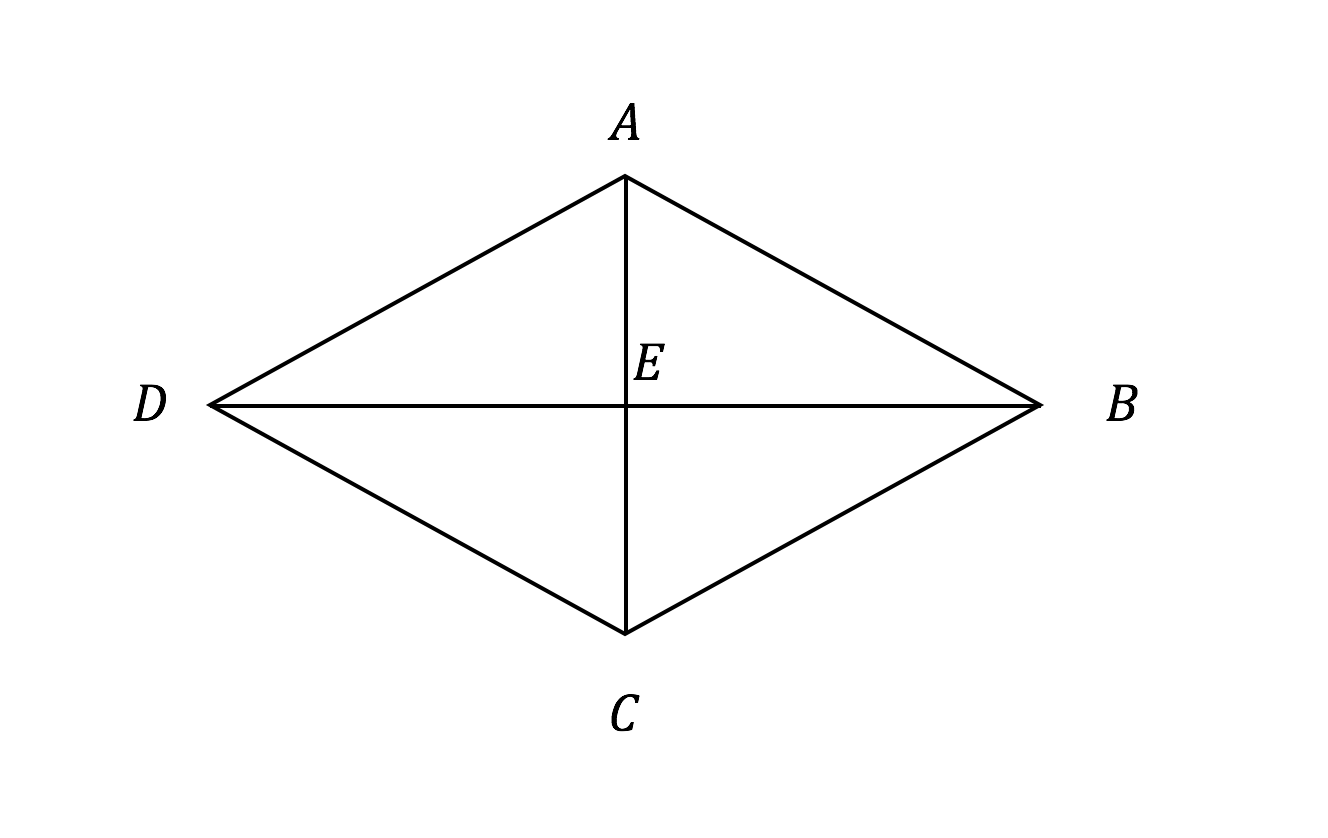
ひし形の4辺はすべて等しいので、 AB=AD ・・・ (1) 平行四辺形の対角線は、それぞれの対角線の中点で交わるので、 BO=DO ・・・ (2) また、AOは共通なので、 AO=AO ・・・ (3) (1), (2), (3)より、3組の辺がそれぞれ等しいので、 ABO≡ ADO 合同な図形の対応する角は等しいので、 ∠AOB=∠AOD ∠AOB+∠AOD=180°だから、 ∠AOB=∠AOD=90° よって、 AC⊥BD 練習問題4直に交わればひし形である abo と ado において 仮定からbo=do ・・・① ∠aob=∠aod・・・② aoは共通 ・・・③ ①~③より 2組の辺とその間の角がそれぞれ等しいから abo≡ ado 合同な図形の対応する辺の長さは等しいからab=ad よって abcdはひし形である o図形の性質と証明(1) 年 組 氏名 No 1 「2つの角が等しい三角形は,二等辺三角形である」ことを次のように証明した。 上の証明の にあてはまる合同条件を,下のアからオまでの中から1つ選びなさ



ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
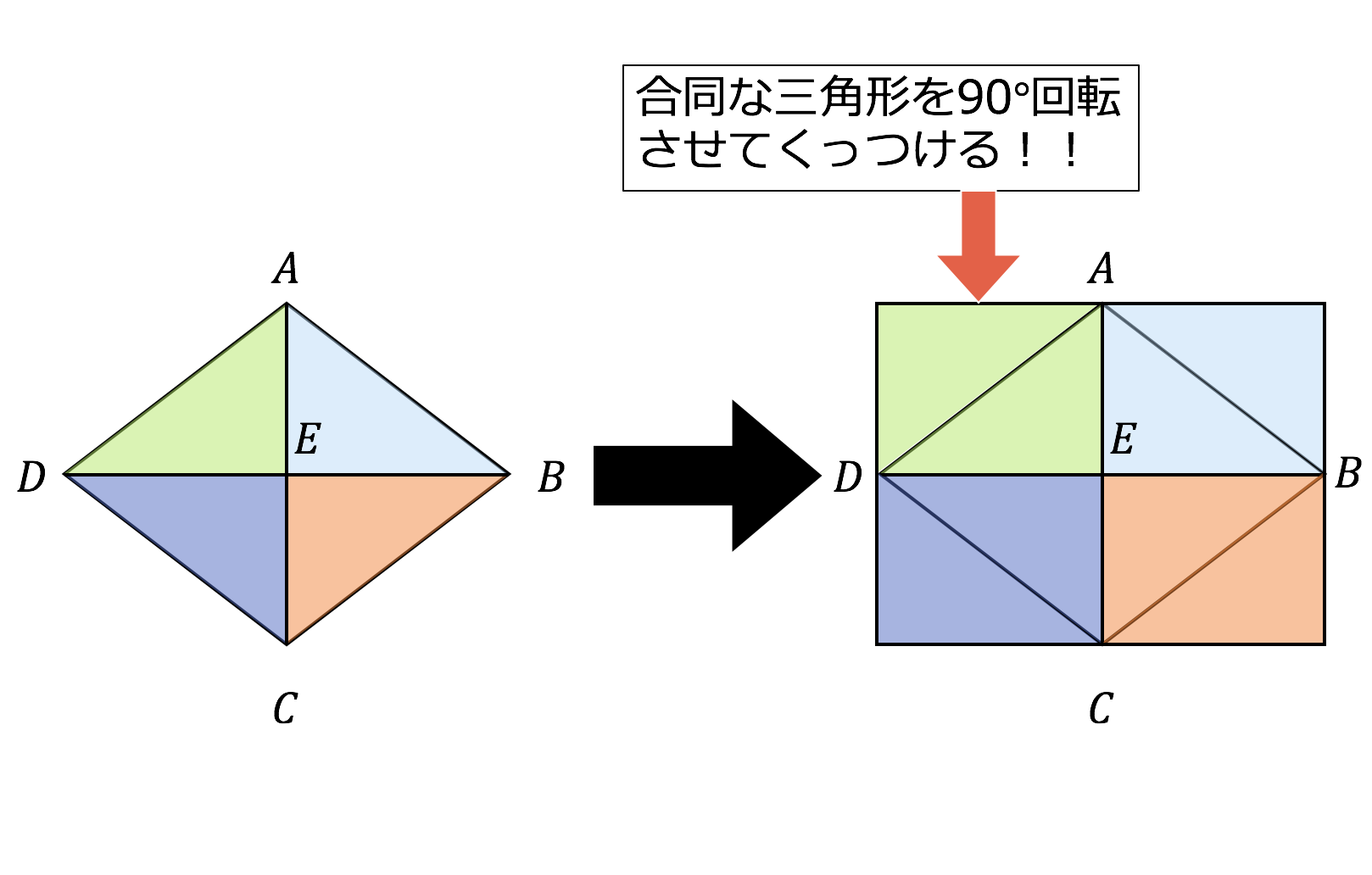
16年8月23日 / Last updated 16年8月23日 parako 数学 中2数学 四角形の性質と証明 特別な四角形 長方形、ひし形、正方形の定義、性質を使った問題です。 特別な四角形の定義 ひし形→4つの辺が等しい四角形 長方形→4つの角が等しい四角形 正方形→4つの辺が 2 ひし形の性質と面積の公式 3 ひし形の面積の公式の証明(2種類) 31 ひし形の面積の公式の証明①:合同な三角形をくっつける 32 ひし形の面積の公式の証明②:ひし形を4つの直角三角形に分割する 4 ひし形の面積の公式を用いた練習問題(2題) 5 そのためには、 図形の証明で使う最低限の知識(図形の性質、合同条件等)を頭に叩き込んで下さい。大した量ではありません。その後、「証明の書き方」を覚えます。 テンプレート化しちゃうんです。 あとは基本の証明問題を10問練習し模試レベルに移行。



中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋




公式なんて覚えない ひし形の面積は直感的に考えよう
証明の方向性としては、 ABMと ADMの合同を証明していくよ。 Step1 ひし形の定義をつかう ABMと ADMにおいて、 ひし形の定義(4つの辺がすべて等しい)より、 AB = AD・・・ (1) Step2 平行四辺形の性質をつかう ひし形は平行四辺形だから、 平行四辺形の性質 がつかえるね。 対角線は中点でそれぞれ交わる という性質より、 BM = DM・・・ (2) Step3 三角形の合同条件をつ 「ひし形」 とは、 「4つの辺が等しい四角形」(定義) のことですね。そして、ひし形は平行四辺形の一種ですから、 「平行四辺形の定義・性質」 は全て合わせ持った上で、 「対角線が直交する」 という特質を持っていますね。 では、どのような条件が揃えば、その図形は「ひし形」と言え証明できるかどうかを考えてみましょう。 証明を振り返ることで,証明に欠かせない条件や性質が明らかになり,それらを満たせば, 図形を変えても同じ結論が導かれることがわかりましたね。 四角形AECFが平行四辺形になる



3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ



ひし形の面積は 1分でわかる求め方 公式 辺の長さ 対角線との関係
長方形,ひし形,正方形の対角線の性質 問1.答え長方形の対角線の長さは等しいことを証明しなさい。 問2.ひし形の対角線は垂直に交わることを証明しなさい。 (隣の角同士が等しいことをいえば良い)



ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典



平行四辺形の3つの性質とその証明 具体例で学ぶ数学
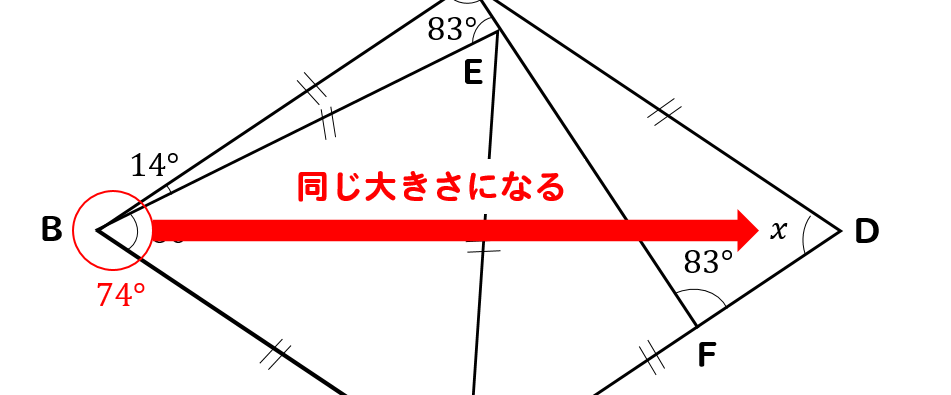



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
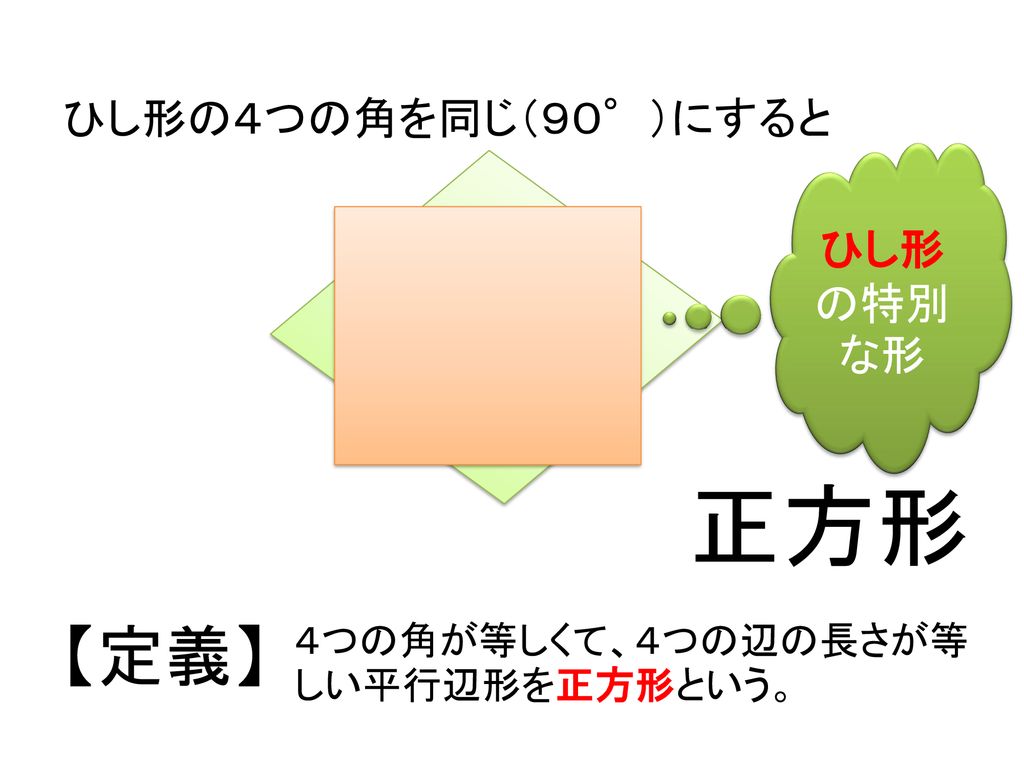



中学校2年生 数学科 図形の性質 Ppt Download



しょうちゃん 公式ブログ 四角形の性質 Powered By Line
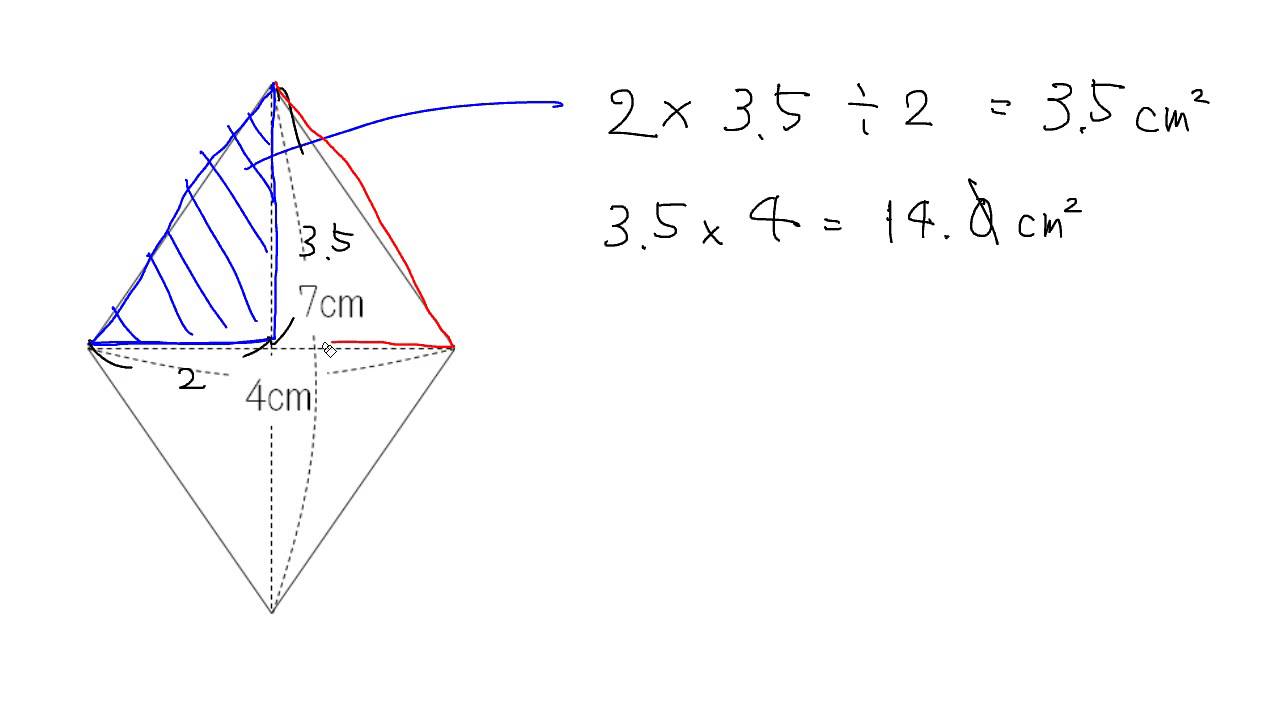



ひし形の面積の公式 Youtube



ひし形の面積の公式 算数の公式




平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ



中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学




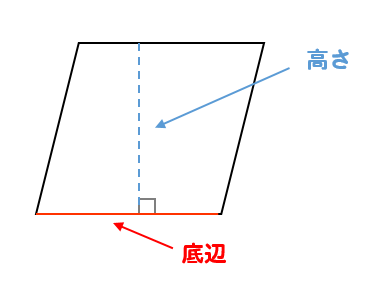
四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



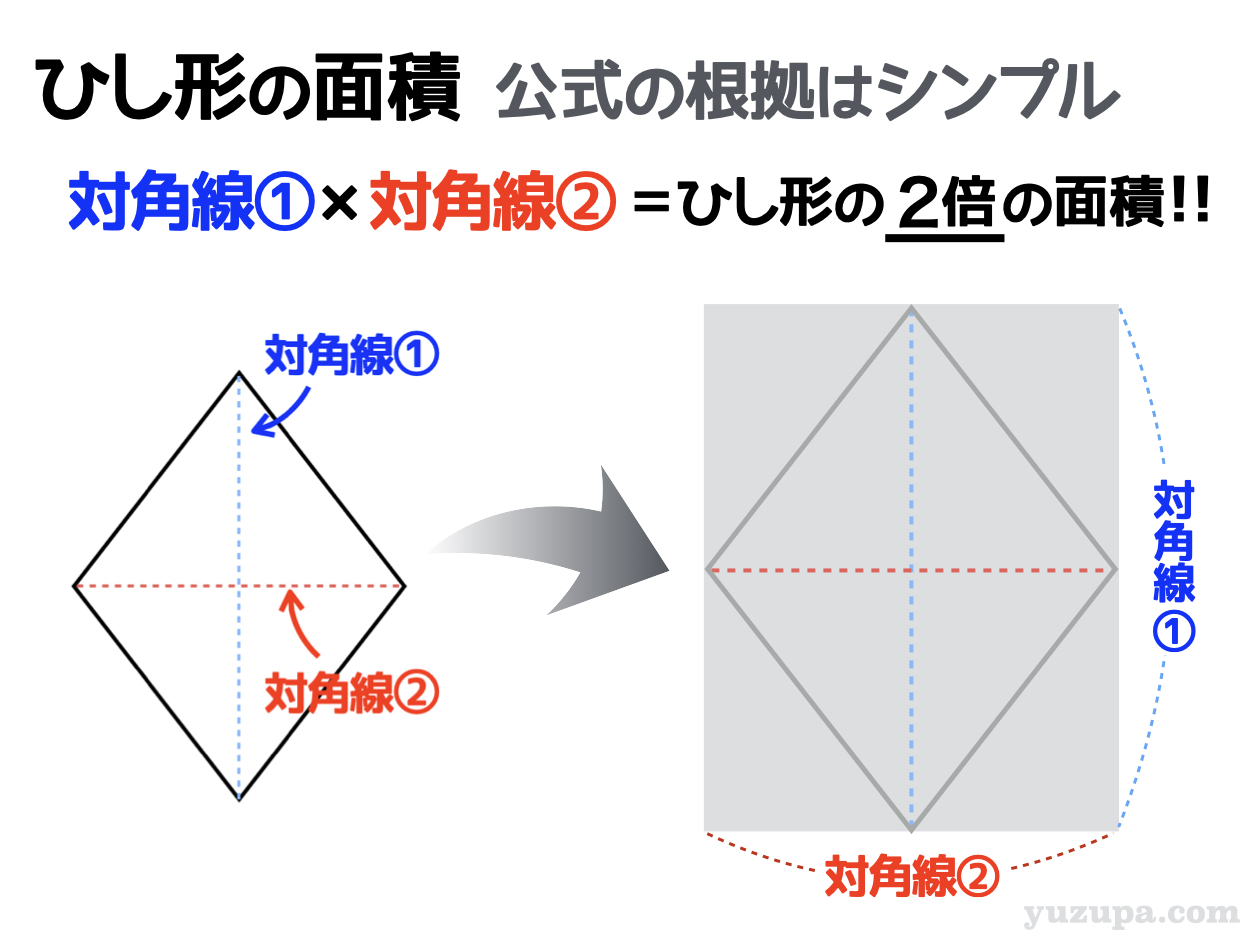
なぜ ひし形の面積は 対角線 対角線 2 なのか を説明します おかわりドリル



中学校2年生 数学科 図形の性質 Ppt Download




条件は長方形 ひし形 正方形 全部当てはまってるから3つじゃないんですか な Clearnote




ていねいな中学校数学2年 第91回 ひし形の定義と性質 Youtube



中学校2年生 数学科 図形の性質 Ppt Download




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



ひし形の定義 性質 条件 Youtube




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく



中学2年数学練習問題 平行四辺形 長方形 ひし形 正方形 の性質



ひし形の面積の公式 算数の公式



ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典




ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典




公式なんて覚えない ひし形の面積は直感的に考えよう



中点連結定理を使った平行四辺形であることの証明 教遊者



3



ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典




中学校数学 証明のコツ 四角形の性質



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



世界一わかりやすい数学問題集中2 5章 図形の性質と証明




特別な平行四辺形の定義 性質 問題の解き方を伝授するぞ 数スタ




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




公式なんて覚えない ひし形の面積は直感的に考えよう




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ



ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典



中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋



ひし形の面積の公式 算数の公式




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




ひし形の面積の求め方 公式と計算例



中学数学 作図 垂直二等分線 角の二等分線 中学数学の無料オンライン学習サイトchu Su




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



4年算数 垂直 平行と四角形3ひし形の教え方



ひし形とは 定義や面積の公式 求め方をわかりやすく解説 受験辞典
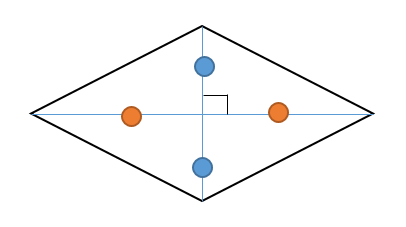



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



中学数学 図形の合同 図形の性質
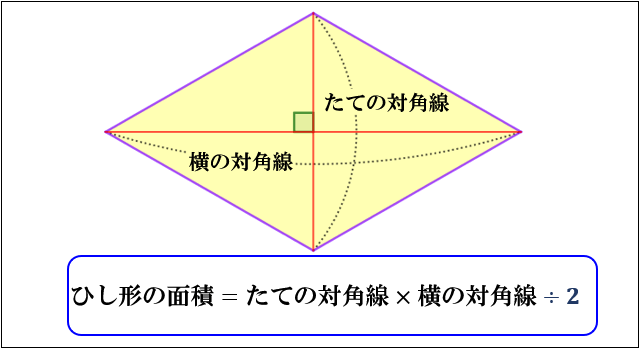



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



四角形の性質 ひし形の性質 平行四辺形の性質 正方形の性質 長方形の性質 女子学院中学 05年 平成17年度 入試算数問題 まいにち一題 中学受験過去問題研究



証明




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




長方形 ひし形 正方形の性質と条件 Youtube




ひし形の性質 対角線はなぜ垂直に交わるのか Qikeru 学びを楽しくわかりやすく




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題
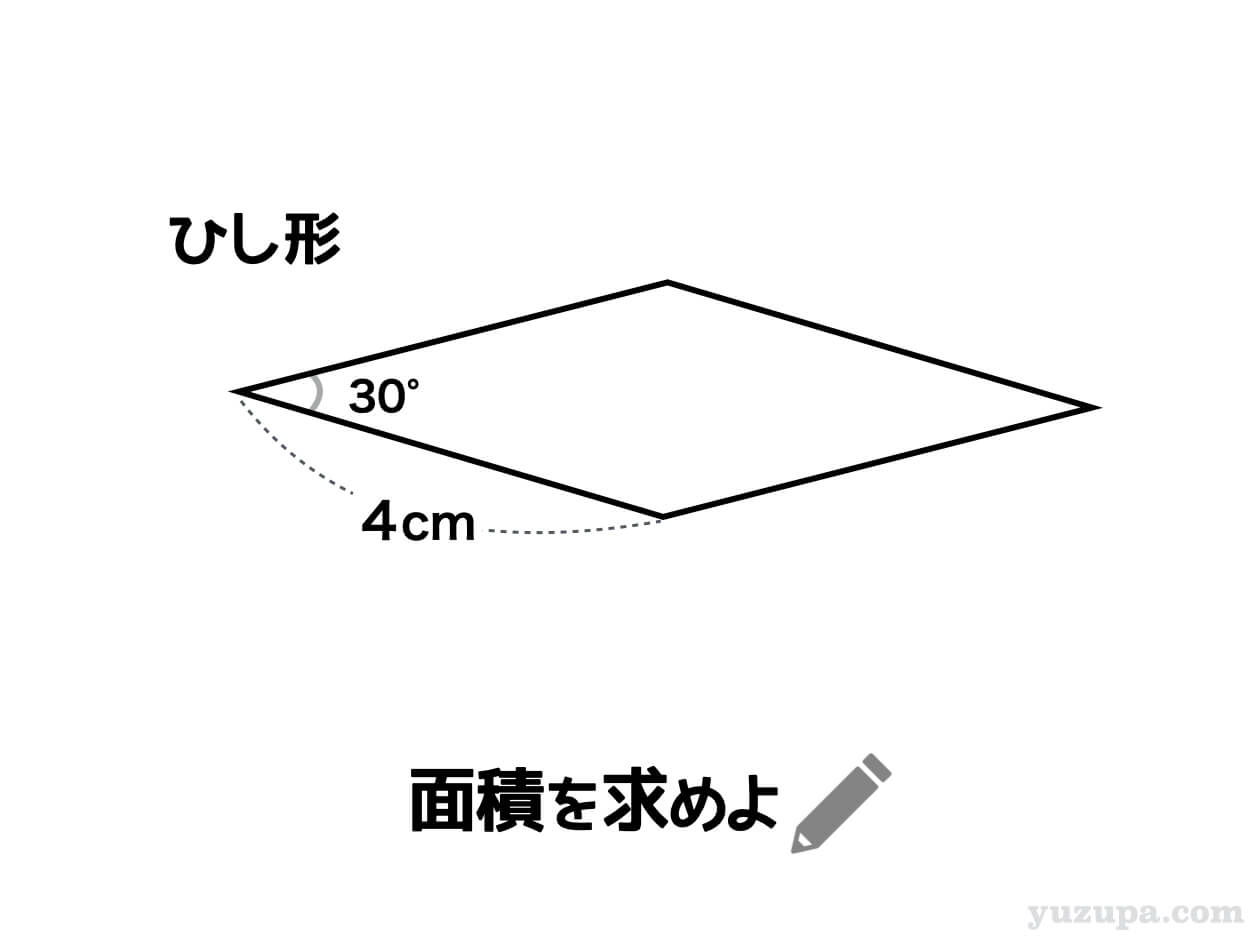



中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋



中学校2年生 数学科 図形の性質 Ppt Download




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ




正三角形の角度 正方形 ひし形との融合問題を解説 数スタ
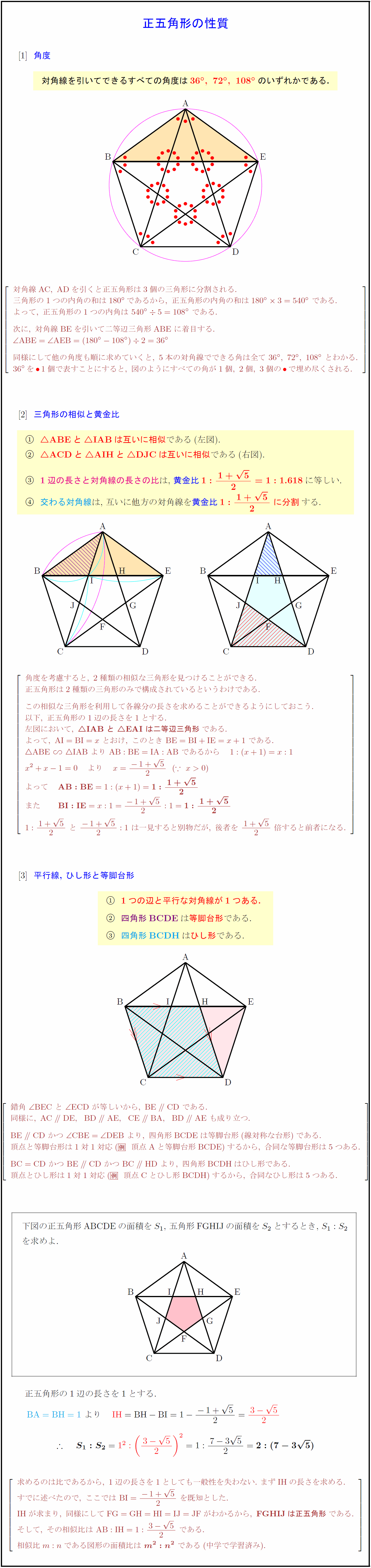



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



3



3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ



1



台形 平行四辺形 ひし形 対角線とは 1 台形 平行四辺形 ひし形 対角線とは 1 台形
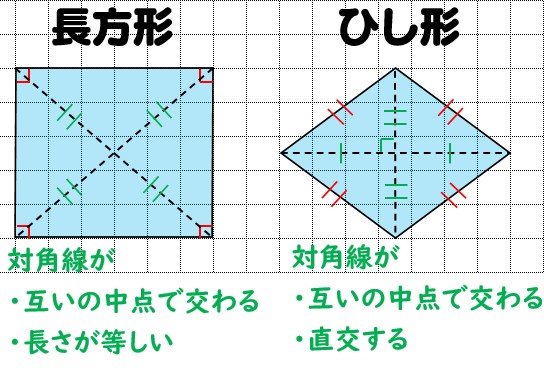



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ
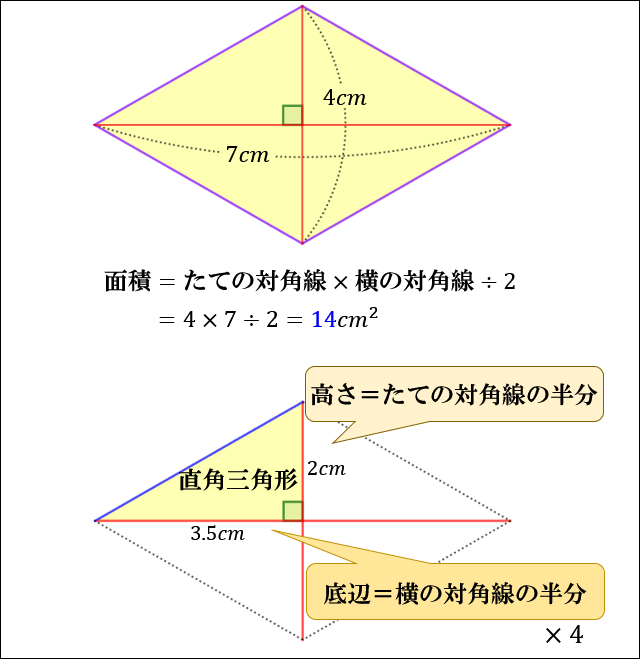



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



ひし形の面積の公式 算数の公式




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
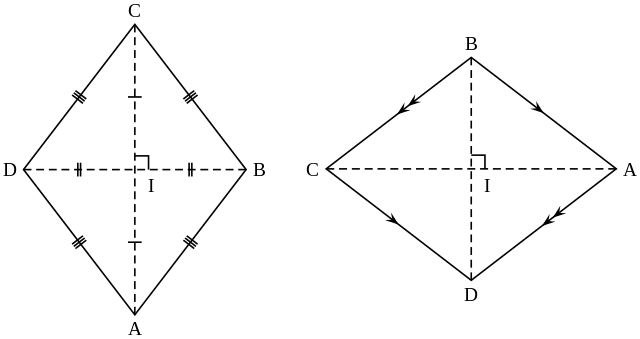



菱形 Wikipedia



1




中学校数学 証明のコツ 四角形の性質




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
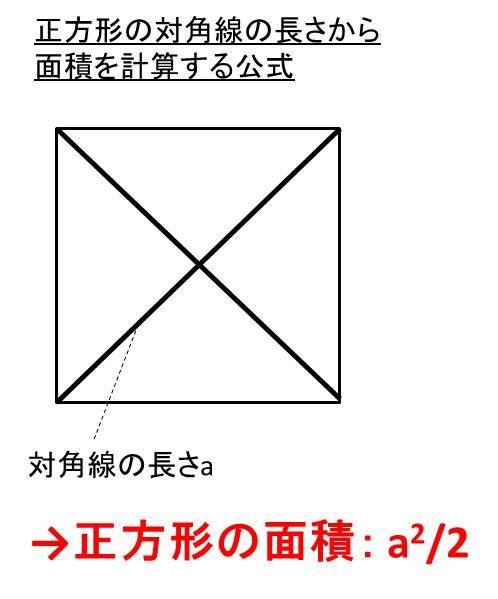



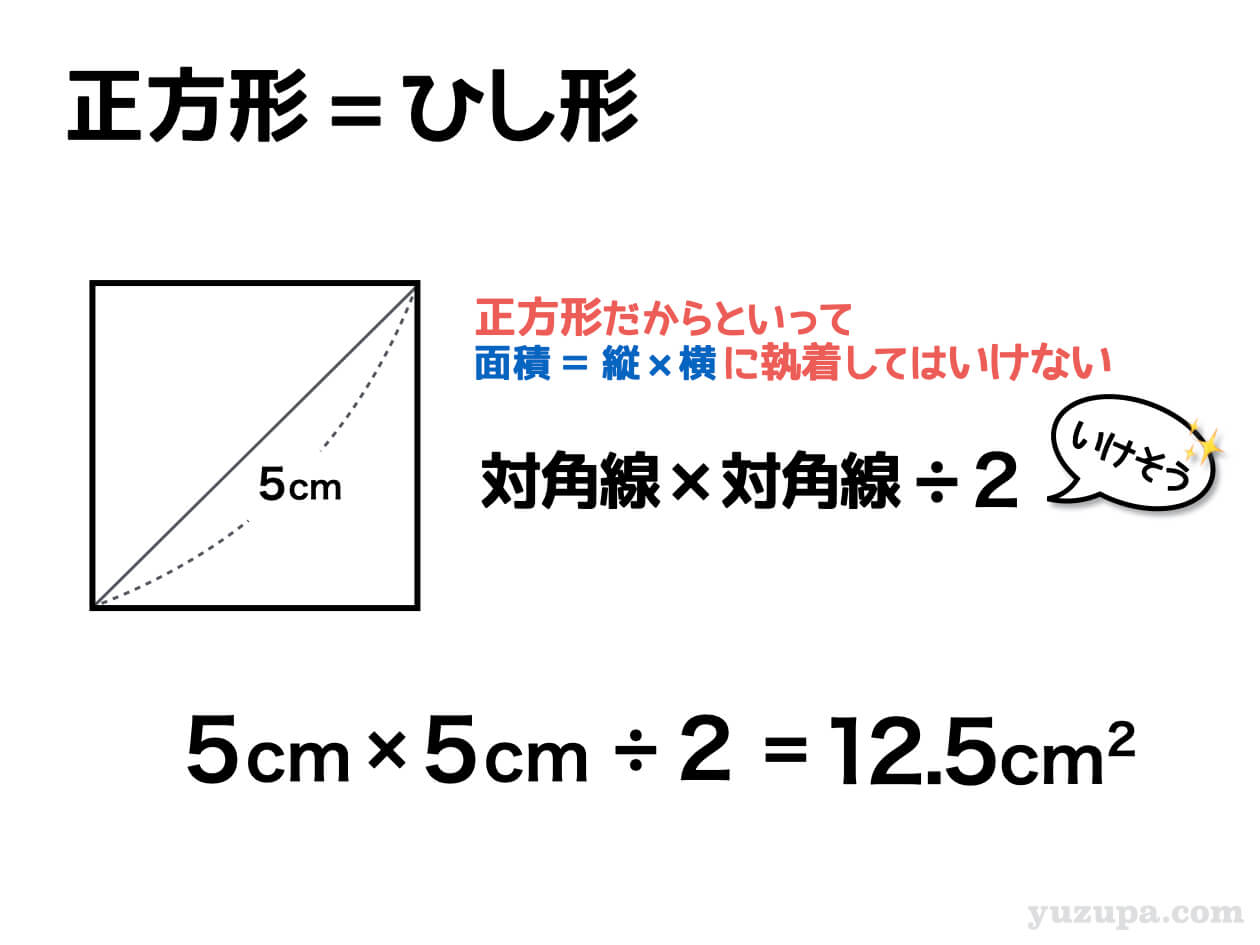
正方形で対角線の長さから面積を計算する方法 面積から対角線を求める公式 平方根 ウルトラフリーダム




3分でわかる ひし形 菱形 の定義 Qikeru 学びを楽しくわかりやすく
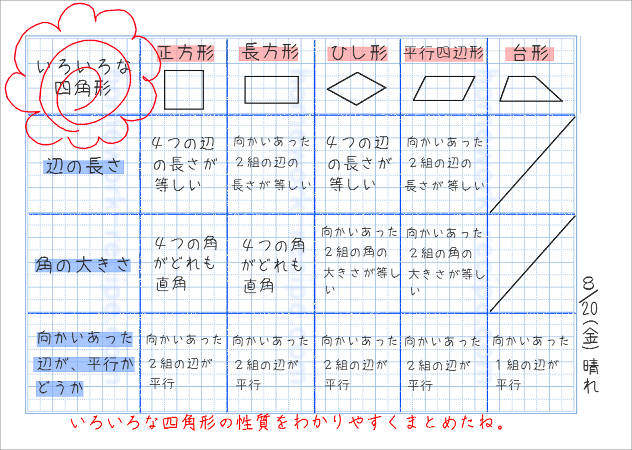



いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ




中2 特別な平行四辺形 長方形 ひし形 正方形の定義と特徴についてイチから Youtube




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題
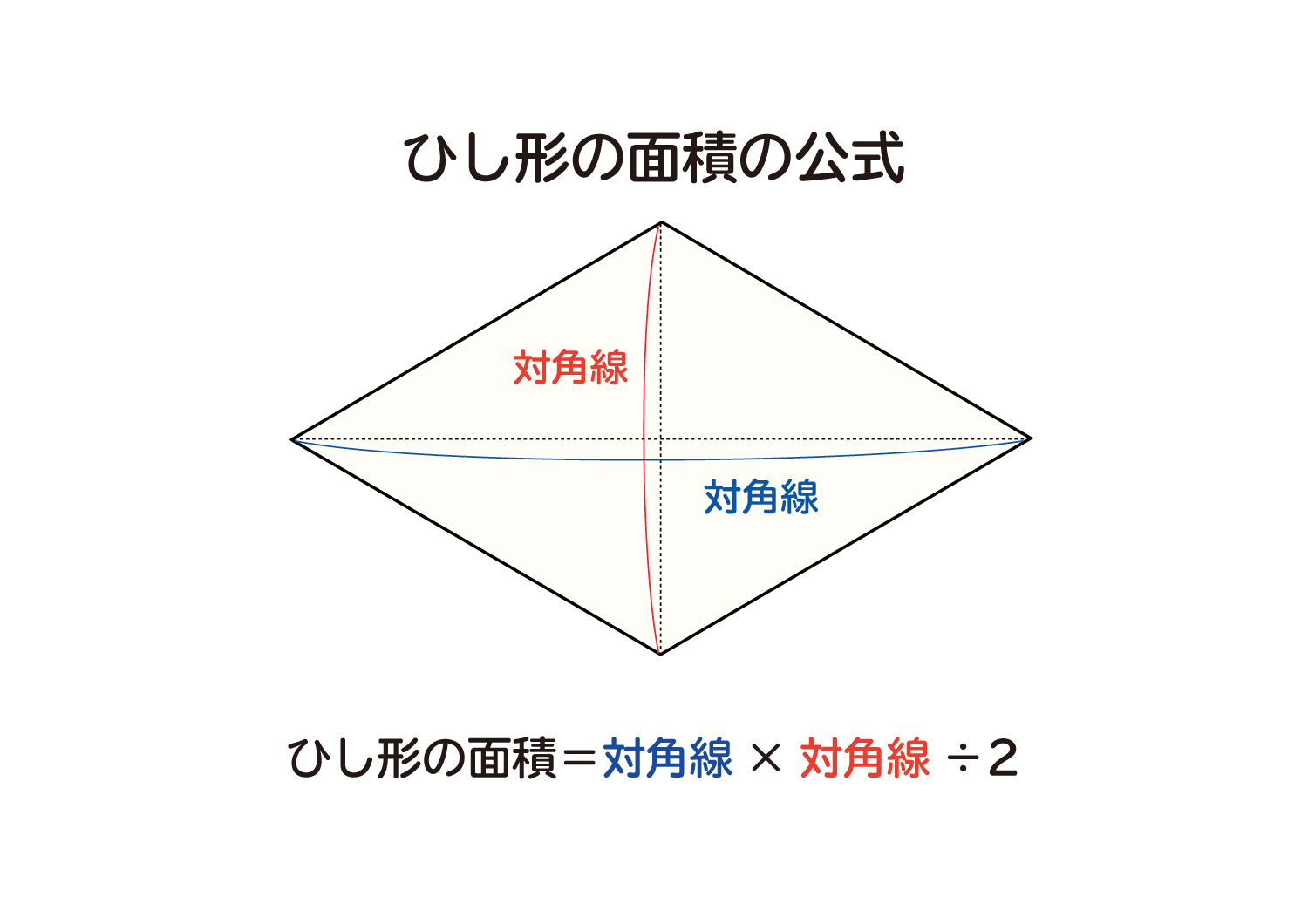



なぜ ひし形の面積は 対角線 対角線 2 なのか を説明します おかわりドリル
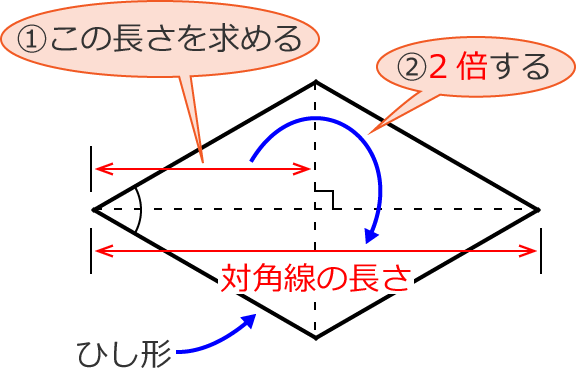



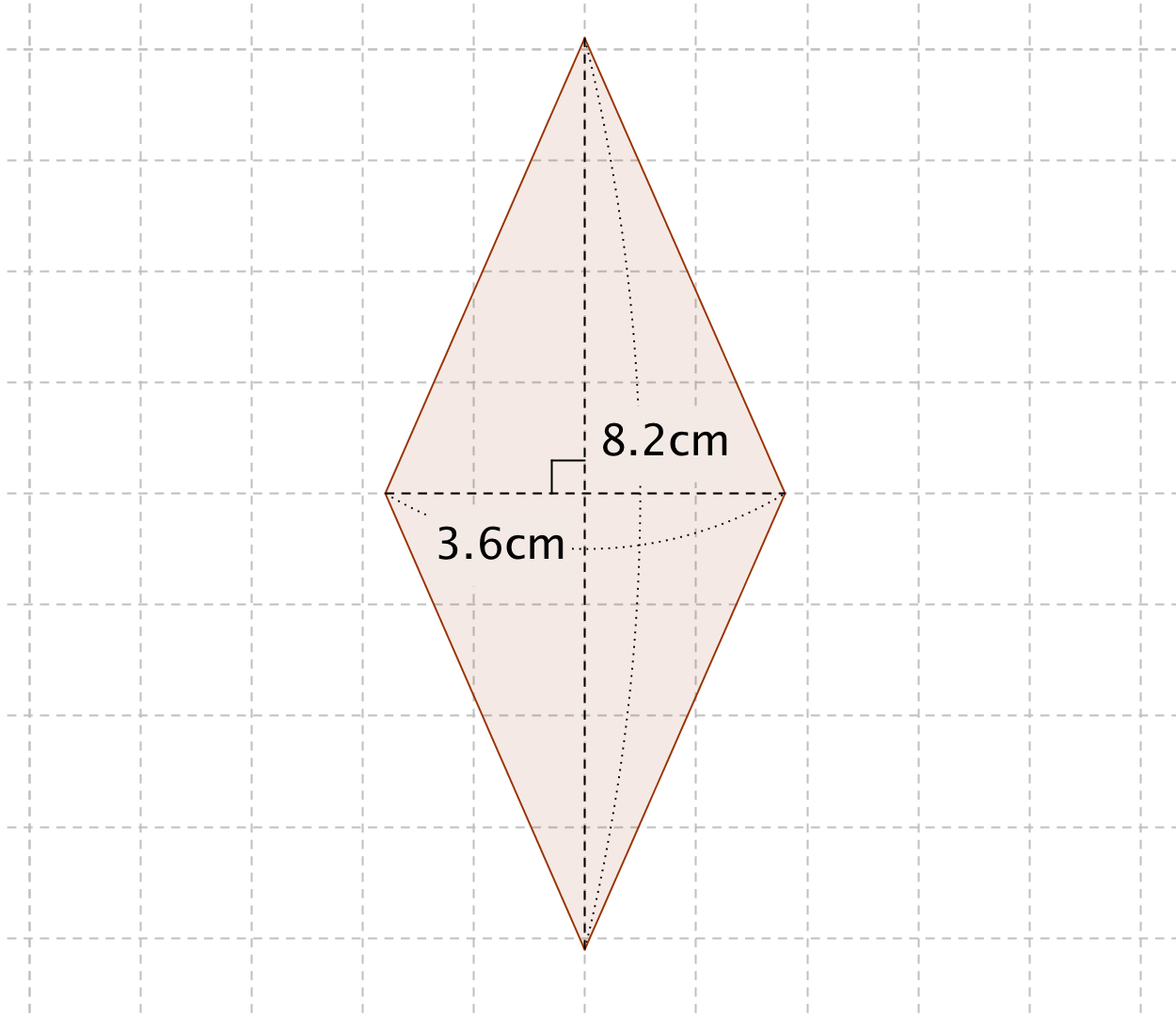
ひし形の対角線の長さの求め方



0 件のコメント:
コメントを投稿