さらに,七角形,八角形,を調べると,次 の通りである。 <七角形の場合> (6 つの内角の和) =(他の1 つの外周角)+540° <八角形の場合> (7 つの内角の和) =(他の1 つの外周角)+7° これらの右辺に着目すると,角の数が増える每个角1度 总共7度 根据某个公式180乘(x2) x是多边形的边数 至于画的方法有一个好的标准的 先作一个点 再虚线任何方向作一个正三角形 接着再沿着那个正三角形的边继续做正三角形 连续作5个 再把外围连接 这个就是正统的正六角形(正六边形)的画法了 希望我能解释得很好。我目前正八角形の1つ分の内角は\(=135°\) 正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法 次は内角の和から1つ分の大きさを求める方法

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
八角形 内角の和
八角形 内角の和-内角の和が180°になるということがわかります。 星形の図形では 三角形の外角の性質を利用していくと 全ての角を1つの三角形に集めることができるので 最終的には、和が180°!ということになります。 正八角形的每个内角是(135°) 根据多边形内角和定理:Sn=(n2)×180°, 因为正八角形有8条边,所以n=8, 所以正八角形的内角和为()×180°=1080° 所以正八角形的每个内角是1080÷8=135° 多边形的公式总结: 1 n边形的内角的和等于(n2)×180° 2



円に内接する八角形の面積 思考力を鍛える数学
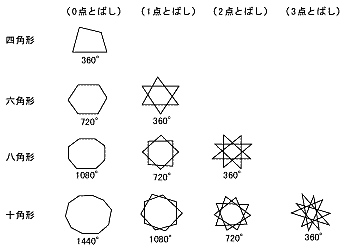
星型八角形は四角形が2つ(7°),星型十角 形は五角形が2つ(1080°)の図形の組み合わせ であり,その内角の和は容易に求められる。 星型多角形の内角の和を次の表にまとめた。 この表から,星型多角形の内角の和は,頂点の一方で、内角の和は先ほど求めたように、180°×3=540°ですね。 さて、外角と内角の和から内角の和を引くと、残るのは外角の和のみになるので、 900°540°=360° となります。 さて、他の多角形についても考えてみましょう! 多角形の外角の和は360°! 正多角形の内角を計算したいんだけど?? こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。 正多角形の内角 を知りたいときってあるよね?? 多角形の内角の和は公式つかえばドヤ顔できるけど、 せ、正多角形の内角はどうすれば・・・?
・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を(5)360(四角形の内角和)+180(一直線)×2 (平野智さん、ごんざえもんさん、cdさん、 他) BCおよびHGの延長線が交わる点をPとします。 四角形ABPHの内角の和 四角形EFQDの内角の和 よって、 四角形ABPHの内角の和+四角形EFQDの内角の和
(1) 三角形の内角の和は何度か。 (2) x角形の内角の和は何度か。 (3) 十角形の内角の和は何度か。 (4) 正八角形の一つの内角は何度か。内角の和・外角の和の証明 なぜn角形の内角の和が180°×(n2)となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習にな求八角形内角的测度之和。 解决方案: 八角形 8 边。所以, n = 8 替代品 8 对于 n 在公式中。 八边形内角的测度之和 = (8 − 2) 180 ° = 6 × 180 ° = 1080 ° 八角形内角的测度之和为 1080 °
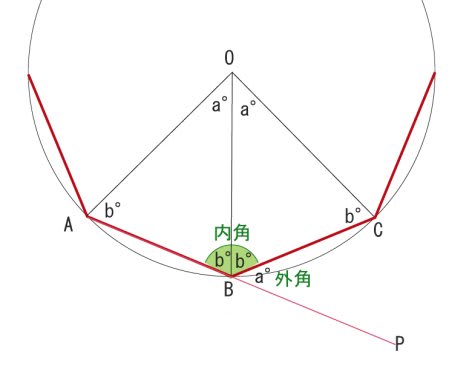



内角 外角 180 どうして 名寄 算数数学教室より
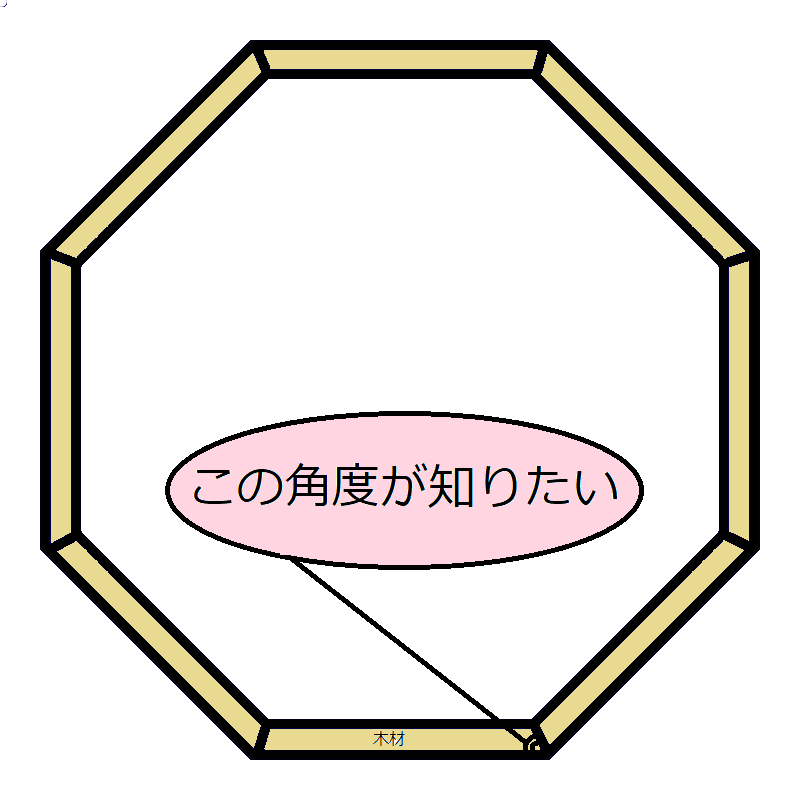



Diy ビニールハウスを作ろう Part4 By Cha Chan Potaru ぽたる
1つの内角の角の大きさは、その図形の内角の和が分かれば、割り算で求められるので、 内角の和は、 「180度×(その図形の辺の数-2)」 で求められるので、 (実際に三角形とかで試すとわかります!!) 正十八角形に当てはめると、 180×(18-2)=←内角の和⑴ 八角形の内角の和は( )度です。 ⑵ 角ア=( )度です。 ⑶ 角イ=( )度です。 図の正八角形は赤い点線に関して線対称なので、AHとBGは平行に なることから考えなさい。(四角形ABGHは台形になります。) ⑷ 角ウ=( )度です。八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;




1 Lihat Cara Penyelesaian Di Qanda



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋
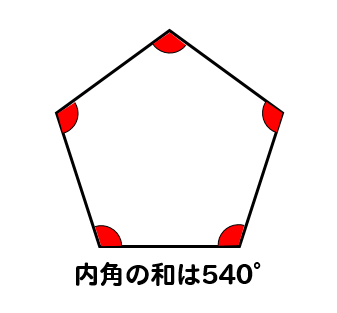
五角形の内角の和は,3つの三角形の内角の 和と等しい。 (2) 説明(例) 図のように,点Pと3つの頂点を結ぶと, 五角形は4つの三角形に分けられる。点Pに おいて五角形の内側に集まっている4つの角 の和は180°だから,五角形の内角の和は,4 つの三角形の内角 (三角形の内角の和) = 180° (四角形の内角の和) = 360° ここまでは大抵の人が知っていると思いますが、六角形や八角形などを覚えている人は少ないかもしれません。 そこで今日は 簡単に覚えられる多角形の内角の和を紹介していこうと思います。 八角形の内角の和の求め方 を紹介していくよ。 よかったら参考にしてみてね^^ 八角形の内角の和を3秒で計算できる公式 8角形の内角の和はチョー簡単。 もうね、一瞬だよ一瞬。 多角形の内角の和の公式をつかっちゃえばね^^ 念のために復習しよう。 n角形
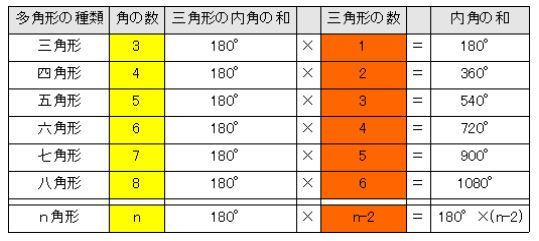



内角攻め それとも外角攻め すうがくラボのブログ



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf
内角の和は,三角形3 つ分だから, 180ß*3=540ß 同様に,n角形の内角の和は, 180ß*(n2) となる。 多角形というときには,右の ようなへこんだ図形は考えな い。 チェック2 多角形の内角の和 教科書 16 多角形の内角と外角 P92~94・101~102(1)九角形の内角の和は何度ですか。 (2)正五角形の1つの内角は何度ですか。 (3)1つの外角が°の正多角形は正何角形ですか。 (4)六角形の対角線の本数は何本ですか。 (5)下の図のアの角度は何度ですか。内角の和 外角の和 正多角形の 1つの内角 対角線 の総数 三角形 180° 360° 60° 0本 四角形 360° 90° 2本 五角形 540° 108° 5本 六角形 7° 1° 9本 七角形 900° 128と4/7 ° 14本 八角形 1080° 135° 本 九角形 1260° 140° 27本 十角形 1440° 144° 35本 十一角形
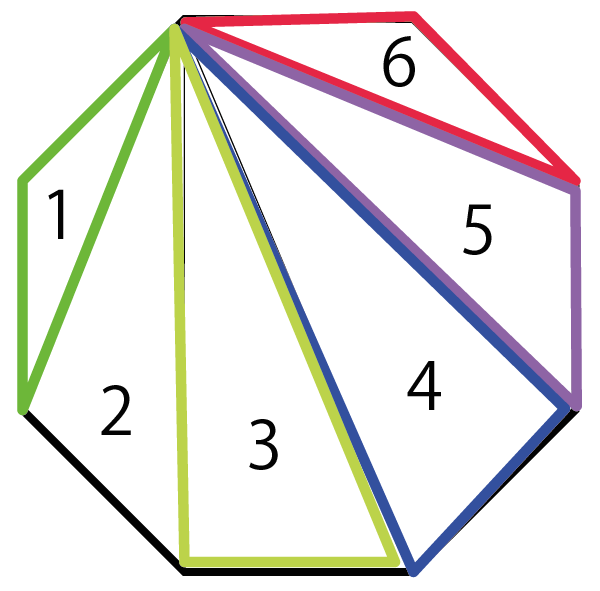



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学
$$360 \div 10=36°$$ 内角は\(180(外角)\)より $$=144°$$ となります。 内角の和を考えて求める場合には $$180 \times (102)=1440°$$ 内角の和をこのように求めて 10で割ってやれば求めることができます。 $$1440 \div 10 =144°$$正10角形は2等辺三角形が10個 出来ますよね?3 星形七角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e+∠f+∠g) 4 星形 n 角形の角の和 星形七角形を,内側の七角形の各辺を延長してできた図形と考える。 内側の七角形のまわりにできた7つの三角形の内角の和の合計は, 180°×7=1260°三角形の内角の和は180°であることを理解することができる。 多角形の内角の和を三角形の内角の和をもとにして求め、考え方を説明することができる。 4 評価規準 算数への 関心・意欲・態度 数学的な考え方 数量や図形についての 技能




内角の和 180 N 2 外角の和 360 教遊者




課題学習の指導 数学
外角は図2のような角では ない 各内角には2つの外角があるが,外角の大きさというときにはそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° に形の数や内角の和を予想する。 数学的活動 表に記入された三角形から六角形までの結 ア 成り立つ事柄を予想する活動 果を参考にして,七角形,八角形,九角形に ついても予想することを促す。 練6 七角形,八角形,九角形の内角の和を確G
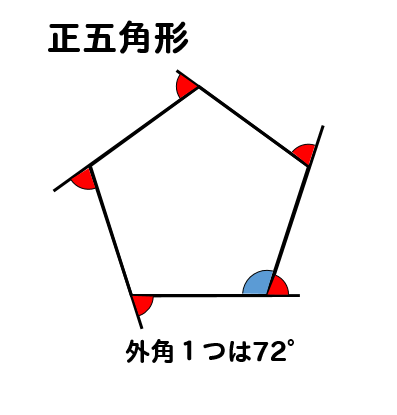



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角
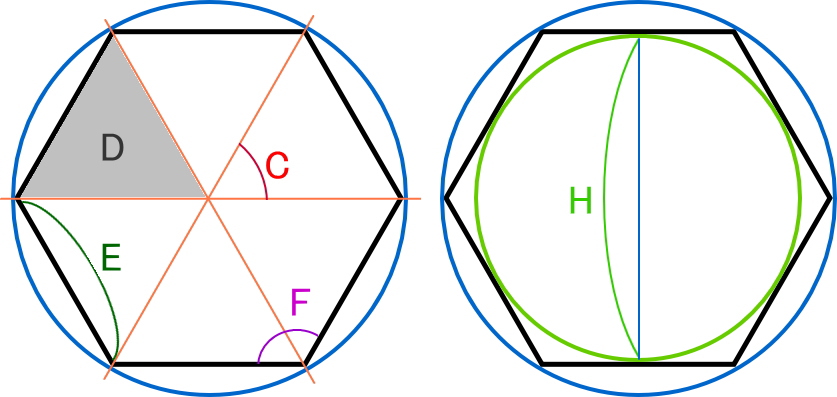



正 角形 正多角形 を表にしてみる エクセル関数の使い方



正八角形の作図 家紋の描き方005a 夏貸文庫




小学校5年 算数 正多角形の角の大きさ Youtube
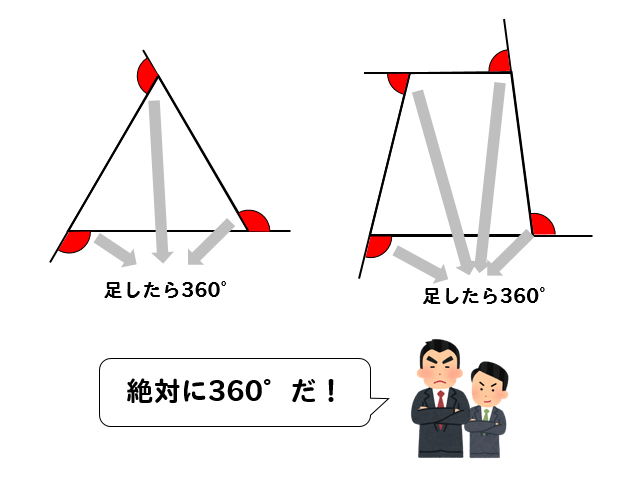



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



Happylilac Net Seitakakkei Ans Pdf



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫




多角形の内角の和 は何度なのか を説明します おかわりドリル




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく



正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



円に内接する八角形の面積 思考力を鍛える数学




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
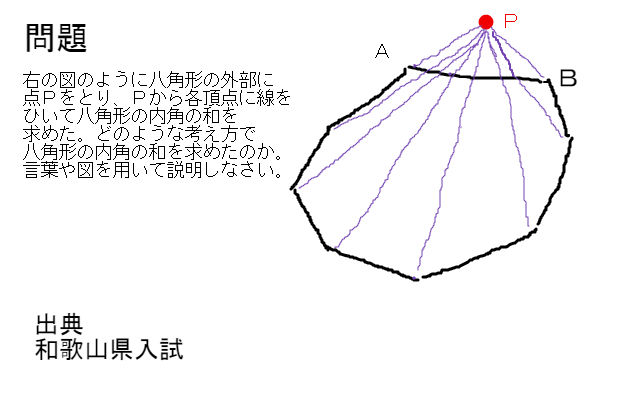



図形問題の徹底演習 八角形の内角の和 中学数学 理科 寺子屋塾の復習サイト



内角の和が540 7 900 1080 1260 の多角形は何角形か



Mathematics 算数のコツ 1 角度の問題は 等しい角を見つけて書き込む 働きアリ The 2nd



3



多角形 中学受験 の問題31題をただひたすら解くページ チャンプルー
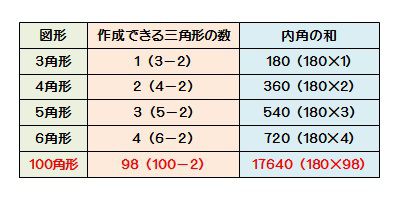



多角形の内角の和 算数の公式覚えてますか




正多角形の1つの内角 外角を求める方法を問題解説 数スタ



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋



Diy製作 正八角形 レシプロカル構造のひさし屋根の設計図を描いてみた 円形屋根 作り方 東京diyスクール




多角形の英語 五角形 六角形 八角形 12角形 正多角形など 英語独学マスター



正8角形 正八角形 の角度の求め方は 1分でわかる内角の和 計算 外角 正9角形の角度




無料 中2数学 基本解説 解答プリント 227 図形7 復習




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 中2数学 Youtube
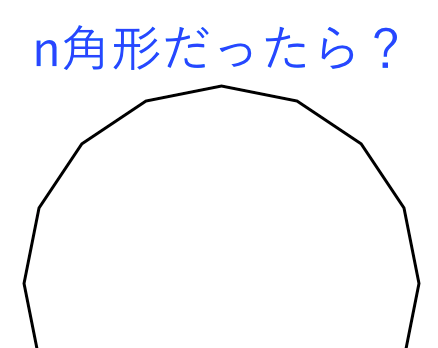



図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に




多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス



1



3



教えてください 正八角形です xの角度の求め方を小学生がわかるよ Yahoo 知恵袋




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



円に内接する八角形の面積 思考力を鍛える数学




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




小5 算数 小5 54 正多角形 Youtube




多角形の内角の和 算数の公式覚えてますか




七十八角形 Wikipedia




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫



正八角形の角度について 図の 印の角度は全部等しいらしいのですがこれはどう Yahoo 知恵袋




正多角形の内角と外角の大きさ 具体例で学ぶ数学




多角形の内角の和 外角の和の公式 数学fun



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
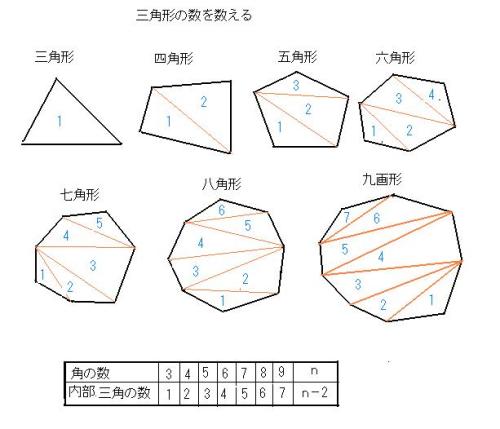



多角形の内角の和を簡単に求める方法 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




内角の和 180 N 2 外角の和 360 教遊者



720度 星形九角形の角度の和



2
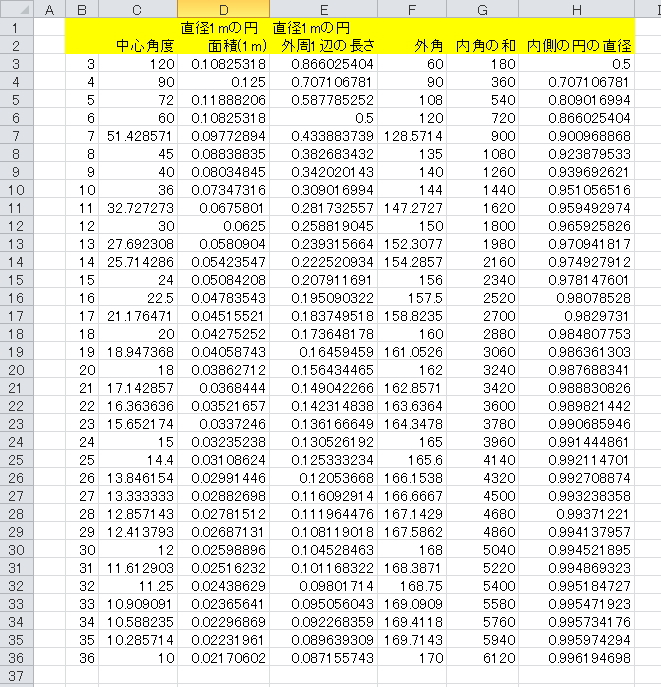



正 角形 正多角形 を表にしてみる エクセル関数の使い方




1 2 31 4 1 5116 6 Lihat Cara Penyelesaian Di Qanda



多角形 中学受験 の問題31題をただひたすら解くページ チャンプルー



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



Www1 Iwate School Jp Action Common Download Main Upload Id 1312
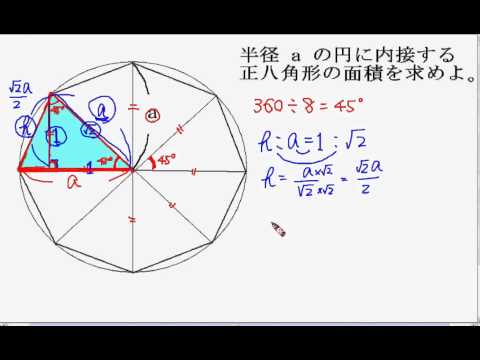



中3数学 正八角形の面積 Youtube




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



1




1 Lihat Cara Penyelesaian Di Qanda




内角の和 180 N 2 外角の和 360 教遊者




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より
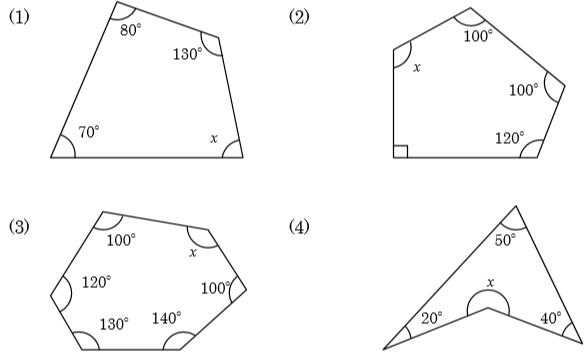



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



十八角形 Wikipedia



多角形の外角の和 On Vimeo




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん



720度 星形九角形の角度の和
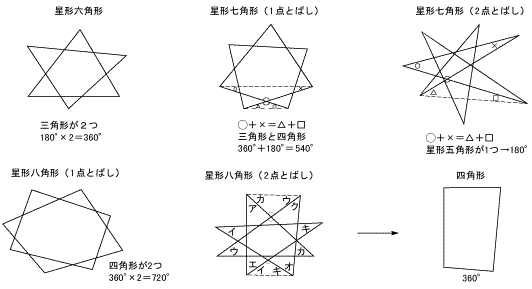



課題学習の指導 数学



Http Www Hpa Kb Site Com Wp Content Uploads 15 02 E5 B9 E9 9d E5 9b E5 E8 92 E5 Ba A6 8 Pdf



正八角形内の角度 渋谷教育学園渋谷中学 受験算数問題より どう解く 中学受験算数




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
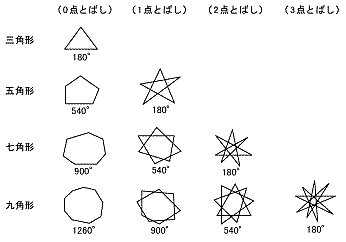



課題学習の指導 数学



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん



720度 星形九角形の角度の和




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




印刷可能 八 角形 の 角度 犬 イラスト




八角形 Wikipedia



2



課題学習の指導 数学




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



正5角形の角度の求め方は 1分でわかる値 内角の和 正6角形 正8角形の角度は




十八角形 Wikipedia



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear




数学 中2 51 多角形の内角と外角の和 基本編 Youtube



正八角形内の角度 渋谷教育学園渋谷中学 受験算数問題より どう解く 中学受験算数



0 件のコメント:
コメントを投稿